Temporal difference

Model free sampling learning. Prediction setting: learn $v_{\pi }$ online from experience under policy $\pi$ Monte Carlo

• Update value $v_n(S_t)$ towards sampled return $G_t$

$$v_{n+1}(S_t)=v_n(S_t)+\alpha (G_t-v_n(S_t))$$

Temporal-difference learning:

• Update value $v_t(S_t)$ towards estimated return $R_{t+1}+\gamma v(S_{t+1})$

$$v_{t+1}(S_t)\leftarrow v_t(S_t)+\alpha (\underset{\text{TD error}}{\underbrace{\stackrel{\text{target}}{\overbrace{R_{t+1}+\gamma v_t(S_{t+1})}}-v_t(S_t)}})$$

• ${\delta }_t=R_{t+1}+\gamma v_t(S_{t+1})-v_t(S_t)$ is called the TD error

Comparison of backup

between dynamic programming, Monte Carlo and Temporal difference.

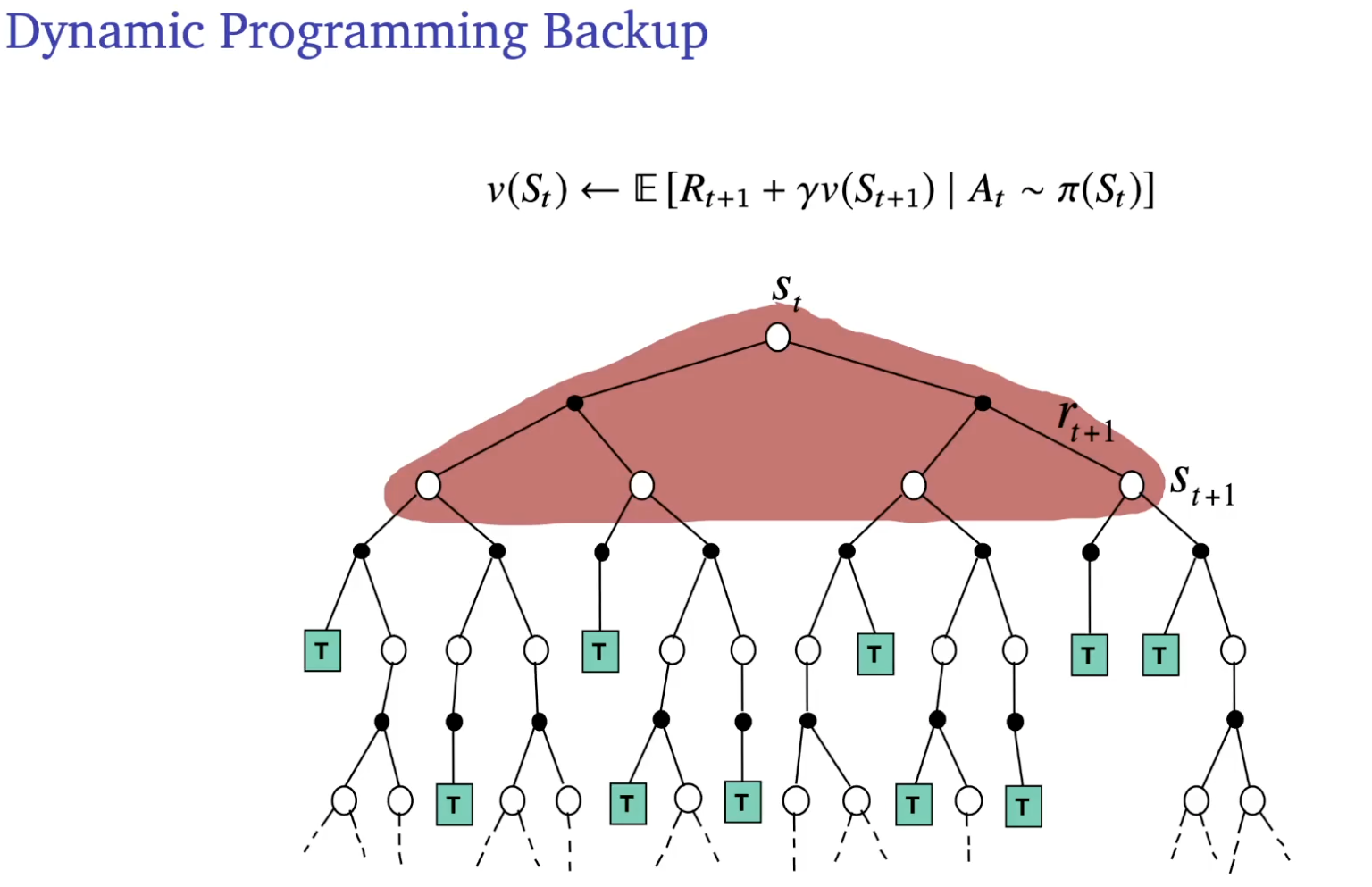
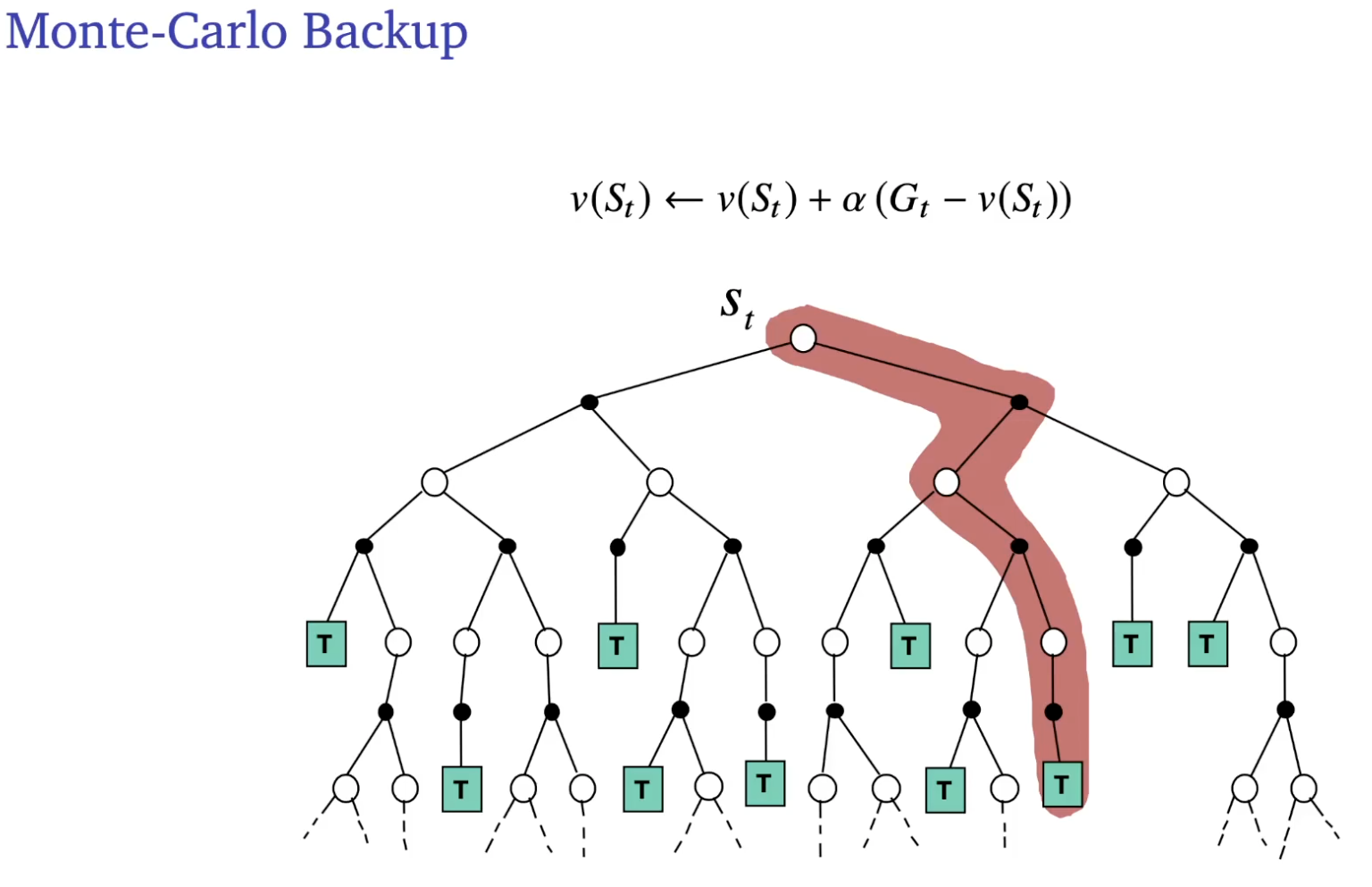
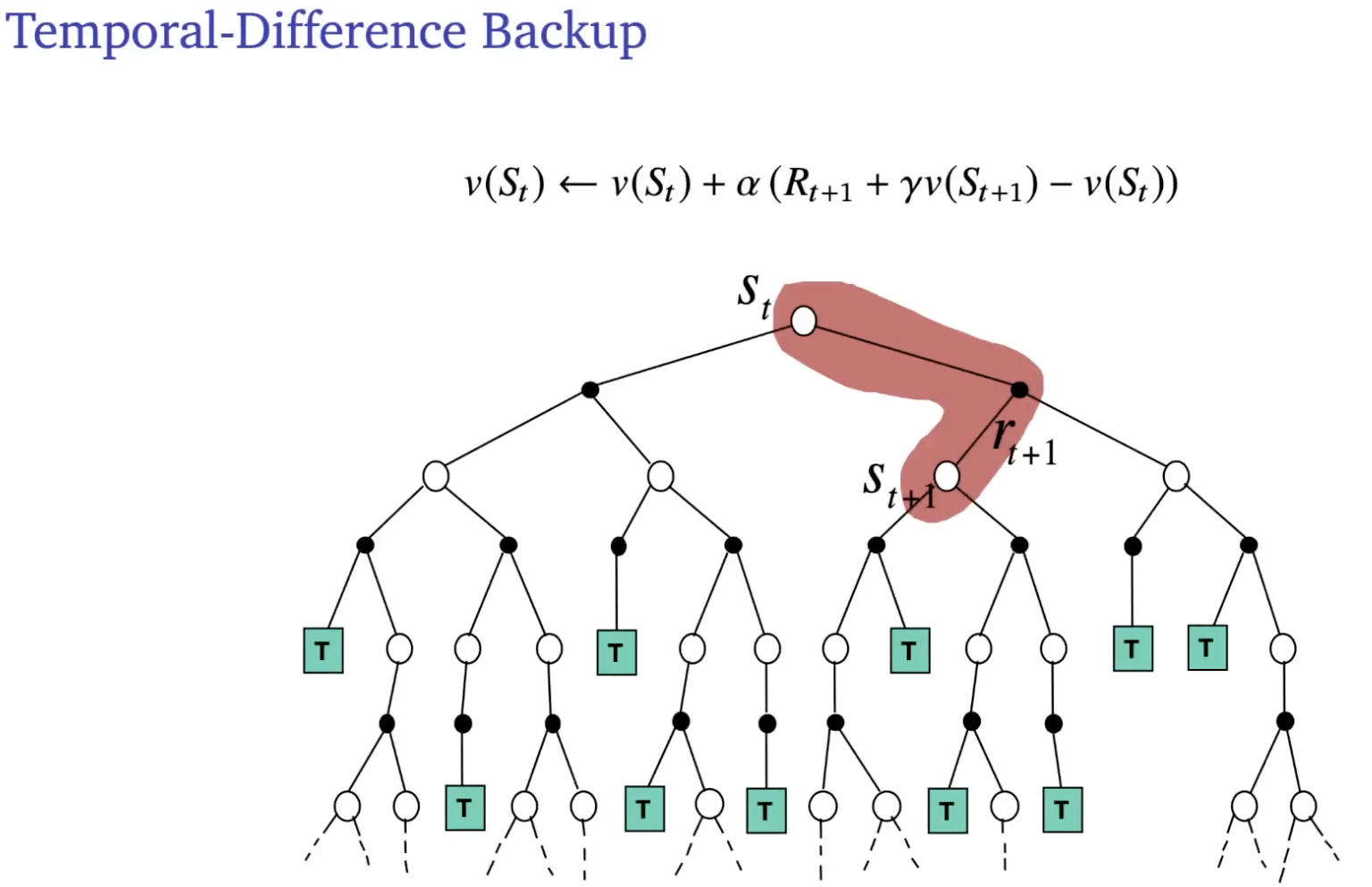
On bootstrapping

We call something bootstrapping if the update involves an estimate. I.e. it need to start from somewhere. Because of that, TD target is a bias estimate. But it has lower variance.

On the convergence

Monte Carlo converges to best mean-squared fit for the observed returns

$$\sum _{k=1}^K\sum _{t=1}^{T_k}{\left(G_t^k-v(S_t^k)\right)}^2$$

TD converges to solution of max likelihood Markov model, given the data. It’s the solution to the empirical MDP $(\mathcal{S},\mathcal{A},\hat{\mathcal{P}},\gamma )$ that best fits the data.

We can kinda see that since TD only do one step.

TD exploits Markov property: can help in fully observable environments. MC does not exploit Markov property: can help in partially-observable environments.

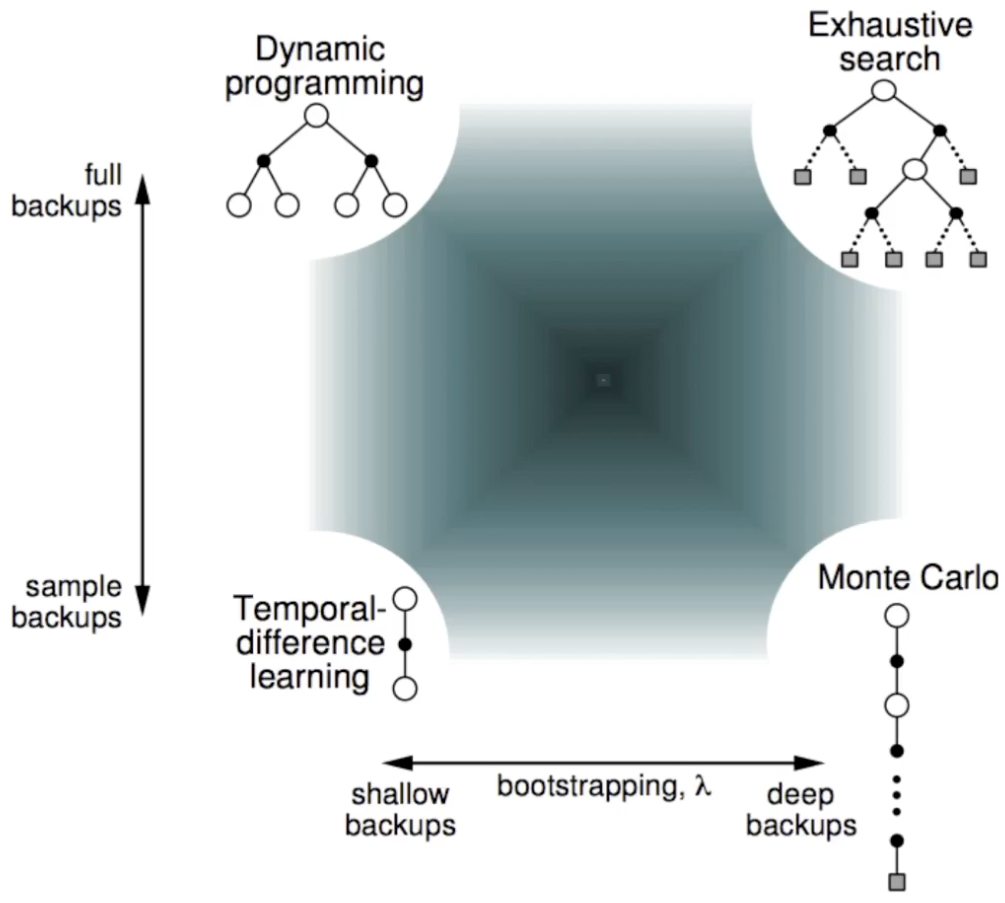
Multi-step returns

Consider the following $n$-step returns for $n=1,2,\infty$:

$$\begin{array}{rcl}n=1& \text{(TD)}& G_t^{(1)}=R_{t+1}+\gamma v(S_{t+1})\\ n=2& & G_t^{(2)}=R_{t+1}+\gamma R_{t+2}+{\gamma }^{2}v(S_{t+2})\\ ⋮& & ⋮\\ n=\infty & \text{(MC)}& G_t^{(\infty )}=R_{t+1}+\gamma R_{t+2}+...+{\gamma }^{T-t-1}{R}_T\end{array}$$

In general, the $n$-step return is defined by

$$G_t^{(n)}=R_{t+1}+\gamma R_{t+2}+...+{\gamma }^{n-1}{R}_{t+n}+{\gamma }^{n}v(S_{t+n})$$

Multi-step temporal-difference learning

$$v(S_t)\leftarrow v(S_t)+\alpha \left(G_t^{(n)}-v(S_t)\right)$$

With good tuning of $\alpha$ and $n$, it can converge faster and better than both MC and TD(0).

Mixing multi-step returns

Mixing bootstrapping and MC:

Multi-step returns bootstrap on one state, $v(S_{t+n})$:

$$\begin{array}{rl}{G}_t^{(n)}& =R_{t+1}+\gamma G_{t+1}^{(n-1)}\text{(while }n>1\text{, continue)}\\ G_t^{(1)}& =R_{t+1}+\gamma v(S_t)\text{.}\text{(truncate \& bootstrap)}\end{array}$$

You can also bootstrap a little bit on multiple states:

$$G_t^{\lambda }=R_{t+1}+\gamma \left((1-\lambda )v(S_{t+1})+\lambda G_{t+1}^{\lambda }\right)$$

This gives a weighted average of $n$-step returns:

$$G_t^{\lambda }=\sum _{n=1}^{\infty }(1-\lambda ){\lambda }^{n-1}{G}_t^{(n)}$$

(Note, ${\sum }_{n=1}^{\infty }(1-\lambda ){\lambda }^{n-1}=1$)

Think about it this way: if we only rely on $G_{t+1}$, that’s MC. If only on bootstrap, that’s TD(0).

Intuition: $1/(1-\lambda )$ is the ‘horizon’, so $\lambda =0.9\approx n=10$.