Policy & value iteration

All things discrete. These are model based methods that plans by dynamic programming to solve a known MDP.

Do things in two steps:

A core idea version:

This can last a long time. And the value may change quite a bit in the big loop but the policy is kept the same. One way to speed it up is to just stop policy evaluation after one sweep (just use next state to update value here) and then do policy update using the max action. So combining both steps tightly. The max can be seen as greedy policy.

Another way to think about it is it use Bellman optimality equation. Note that’s recursive in the next state and this state only too, given we use max everywhere.

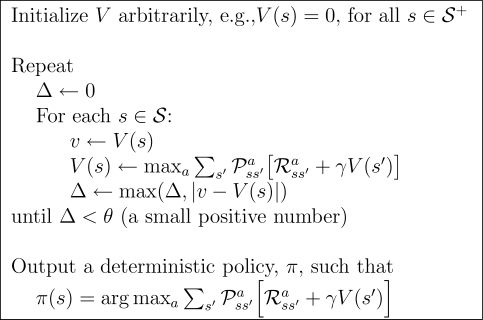
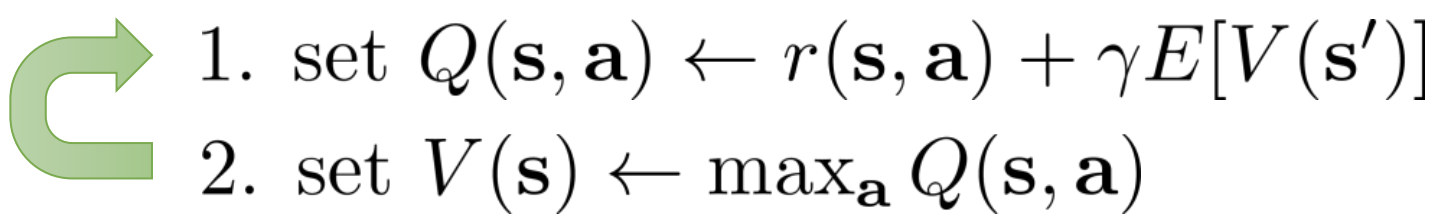
Note now policy iteration and evaluation are in one step and we keep looping.

Why does this work

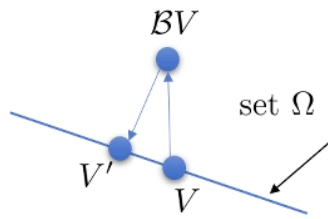
One may ask “hey why does this work though”? See this video. We can show that the bellman update can be formulated as Bellman operator, and the operator is a $\gamma$-contraction mapping, meaning it converges to the unique fixed point.

It’s also covered in CS 285, lecture 7. $\begin{array}{r}\mathcal{B}V=\underset{\mathbf{a}}{\max }{r}_{\mathbf{a}}+\gamma {\mathcal{T}}_{\mathbf{a}}V\end{array}$

• $r_{\mathbf{a}}$: stacked vector of rewards at all states for action $\mathbf{a}$
• ${\mathcal{T}}_{\mathbf{a}}$: matrix of transitions for action $\mathbf{a}$ such that ${\mathcal{T}}_{\mathbf{a},i,j}=p({\mathbf{s}}^{\prime }=i|\mathbf{s}=j,\mathbf{a})$

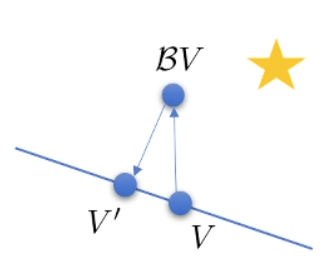
Note that this does not work for the non-tablular case. You can image NN is optimizing by doing a projection $\Pi$ onto a set $\Omega$ (all value functions represented by NN): $V\leftarrow \Pi \mathcal{B}V$. You can see it may get us further from the goal (the star)

---

Policy Gradient can be seen as a soft form of policy iteration. See TRPO for more info.