Q learning

See also Deep Q Recall dynamic programming algorithms Policy & value iteration

$$\begin{array}{rlrl}{v}_{k+1}(s)& =\mathbb{E}\left[R_{t+1}+\gamma v_k(S_{t+1})\mid S_t=s,A_t\sim \pi (S_t)\right]& & \text{(policy evaluation)}\\ v_{k+1}(s)& =\underset{a}{\max }\mathbb{E}\left[R_{t+1}+\gamma v_k(S_{t+1})\mid S_t=s,A_t=a\right]& & \text{(value iteration)}\\ q_{k+1}(s,a)& =\mathbb{E}\left[R_{t+1}+\gamma q_k(S_{t+1},A_{t+1})\mid S_t=s,A_t=a\right]& & \text{(policy evaluation)}\\ q_{k+1}(s,a)& =\mathbb{E}\left[R_{t+1}+\gamma \underset{a^{\prime }}{\max }{q}_k(S_{t+1},a^{\prime })\mid S_t=s,A_t=a\right]& & \text{(value iteration)}\end{array}$$

We have the analogous model -free TD algorithms:

$$\begin{array}{rl}{v}_{t+1}(S_t)& =v_t(S_t)+{\alpha }_t\left(R_{t+1}+\gamma v_t(S_{t+1})-v_t(S_t)\right)\text{(TD)}\\ q_{t+1}(s,a)& =q_t(S_t,A_t)+{\alpha }_t\left(R_{t+1}+\gamma q_t(S_{t+1},A_{t+1})-q_t(S_t,A_t)\right)\text{(SARSA)}\\ q_{t+1}(s,a)& =q_t(S_t,A_t)+{\alpha }_t\left(R_{t+1}+\gamma \underset{a^{\prime }}{\max }{q}_t(S_{t+1},a^{\prime })-q_t(S_t,A_t)\right)\text{(Q-learning)}\end{array}$$

Of course the value iteration on state $v$ cannot be sampled, so there’s no TD algorithm.

Q learning is an Off-Policy algorithm. It estimates the value of the greedy policy

$$q_{t+1}(s,a)=q_t(S_t,A_t)+{\alpha }_t\left(R_{t+1}+\gamma \underset{a^{\prime }}{\max }{q}_t(S_{t+1},a^{\prime })-q_t(S_t,A_t)\right)$$

Acting greedy all the time would not explore sufficiently.

It’s soundness depend on a new theorem:

Q-learning control converges to the optimal action-value function, $q\to q^{\ast }$, as long as we take each action in each state infinitely often.

This is different from GLIE: the policy doesn’t need to converge to greedy. Works for any policy that eventually selects all actions sufficiently often (Requires appropriately decaying step sizes ${\sum }_t{\alpha }_t=\infty$, ${\sum }_t{\alpha }_t^2<\infty$, E.g., $\alpha =1/t^{\omega }$, with $\omega \in (0.5,1)$)

A comparison of SARSA and Q learning

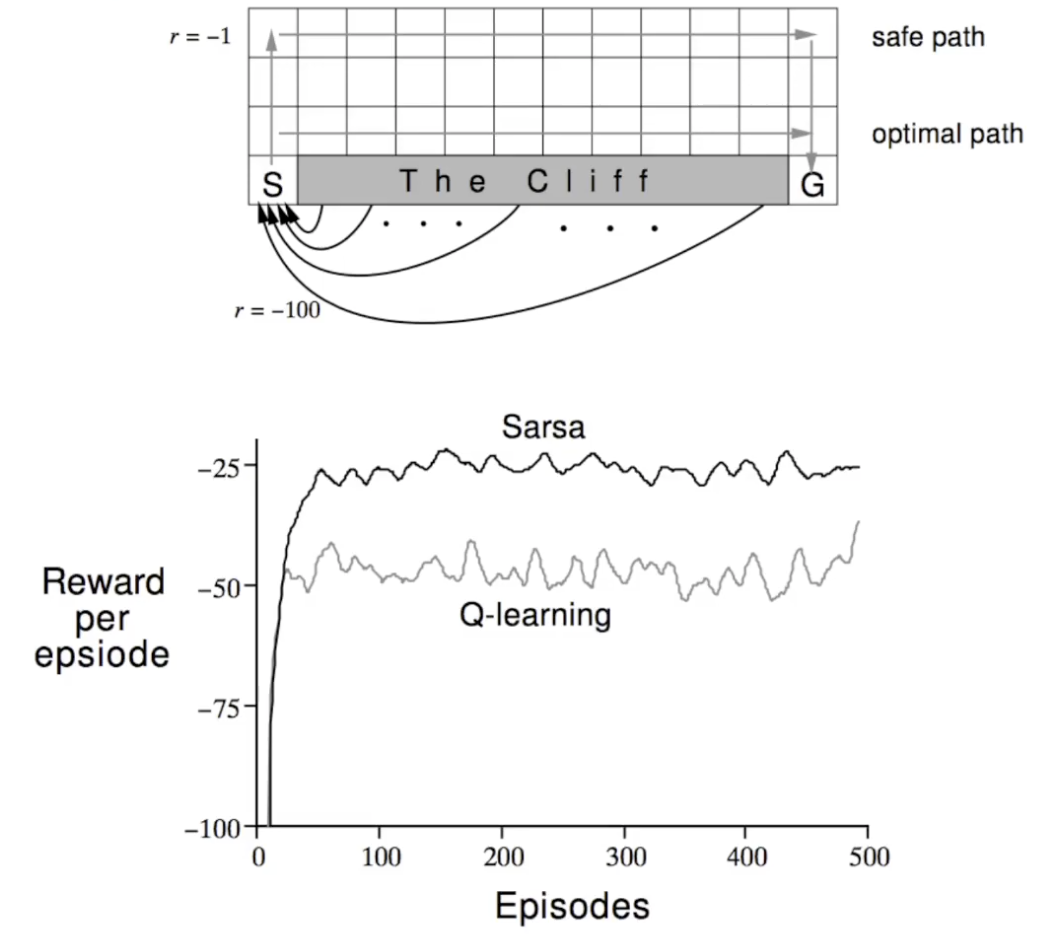In training time, SARSA gets higher reward since it learns that walking on the edge is dangerous, and it learns a safer path. Recall it’s using $ϵ$-greedy for both prediction and control. On the other hand, Q learning would stick to the optimal path, since according to its value estimation the optimal path is just the better one, since it has a larger $max$. So it would explore that path more often and got down more often. Note the final policy may be a more optimal one.

Overestimation

Recall

$$\underset{a}{\max }{q}_t(S_{t+1},a)=q_t(S_{t+1},\arg \underset{a}{\max }{q}_t(S_{t+1},a))$$

Uses same values to select and to evaluate. … but values are approximate

• more likely to select overestimated values
• less likely to select underestimated values

That “max” is persisting. Imagine you are in a state with 100 actions with stochastic outcome. If one of the action by chance got jackpot, then you would keep exploring that state. That leads to super slow convergence: blinded by overestimated values.

Another way to think about it: say we have two random variables: $X_1$ and $X_2$,

$$E[\max (X_1,X_2)]\ge \max (E[X_1],E[X_2])$$

our q estimation is a noisy estimation, and we are using the left one to estimate the right.

Double Q-learning

Store two action-value functions: $q$ and $q^{\prime }$

$$R_{t+1}+\gamma q_t^{\prime }(S_{t+1},\arg \underset{a}{\max }{q}_t(S_{t+1},a))\text{\hspace{1em}(1)}$$ $$R_{t+1}+\gamma q_t(S_{t+1},\arg \underset{a}{\max }{q}_t^{\prime }(S_{t+1},a))\text{\hspace{1em}(2)}$$

Each $t$, pick $q$ or $q^{\prime }$ (e.g., randomly) and update using (1) for $q$ or (2) for $q^{\prime }$.

This solves the issue because now the noise is decorrelated. The “max” when selecting the action may not actually leads to the “max” when actually getting the estimated Q value.

We can also extend this to SARSA.