Switch Transformers

This can be seen as a direct successor of the vanilla MoE, applying this to OG Transformer with tweaks on loss.

There’s also a GShard paper in between, which according to Mixture of Experts Explained, introduces the two new idea:

• Random routing: in a top-2 setup, we always pick the top expert, but the second expert is picked with probability proportional to its weight.
• Expert capacity: we can set a threshold of how many tokens can be processed by one expert. If both experts are at capacity, the token is considered overflowed, and it’s sent to the next layer via residual connections (or dropped entirely in other projects). This concept will become one of the most important concepts for MoEs. Why is expert capacity needed? Since all tensor shapes are statically determined at compilation time, but we cannot know how many tokens will go to each expert ahead of time, we need to fix the capacity factor.

Now back to this one. Only the FFN is being converted to MoE layer. This is the same as GShard.

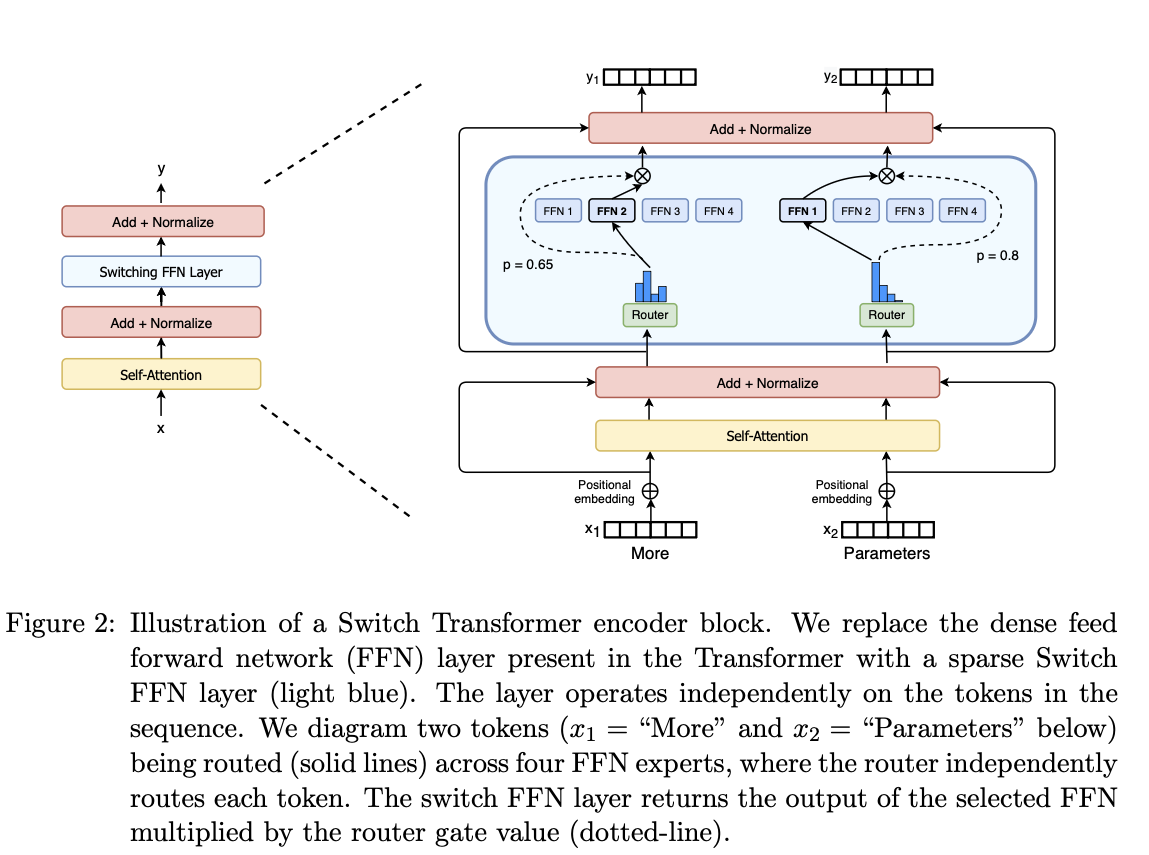
Single expert

Recall in the vanilla MoE, k experts are picked and the results are added together. Here the author argue a single expert is enough.That’s where the name “switch” comes from. The reaons

• Routing computation is reduced
• Batch size can be at least halved
• Routing implementation is simplified and communication costs are reduced. In summary, all because of infra. This is a pragmatic paper.

Efficient Sparse Routing

$$\text{expert capacity}=\left(\frac{\text{tokens per batch}}{\text{number of experts}}\right)\times \text{capacity factor}$$

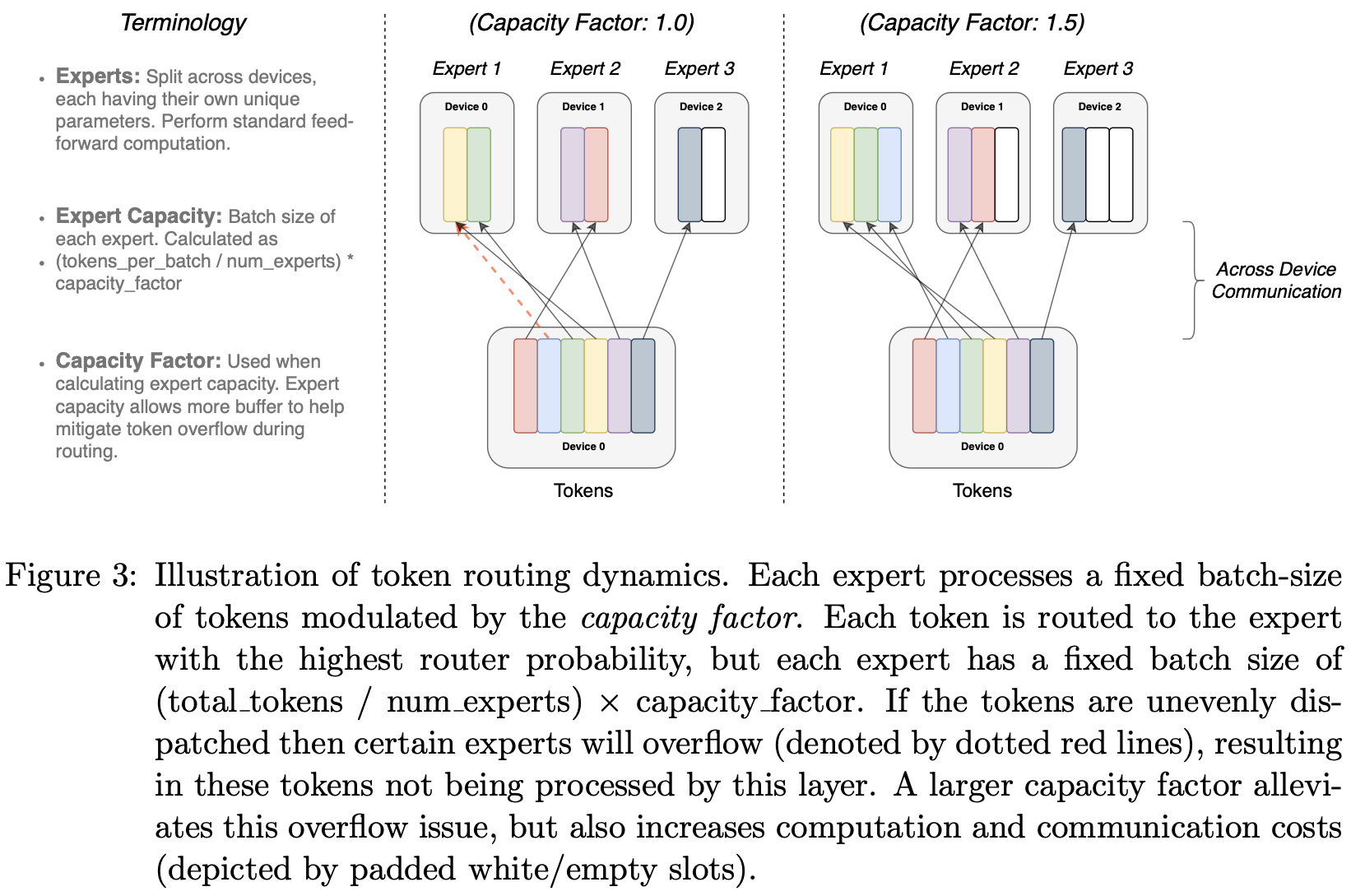
If too many tokens are routed to an expert (referred to later as dropped tokens), computation is skipped and the token representation is passed directly to the next layer through the residual connection.

switch_transformers, page 7 Later in the experiment they show that

Switch Transformers perform better at lower capacity factors (1.0, 1.25). Smaller expert capacities are indicative of the scenario in the large model regime where model memory is very scarce and the capacity factor will want to be made as small as possible

switch_transformers, page 8

What they thought would make it better but didn’t

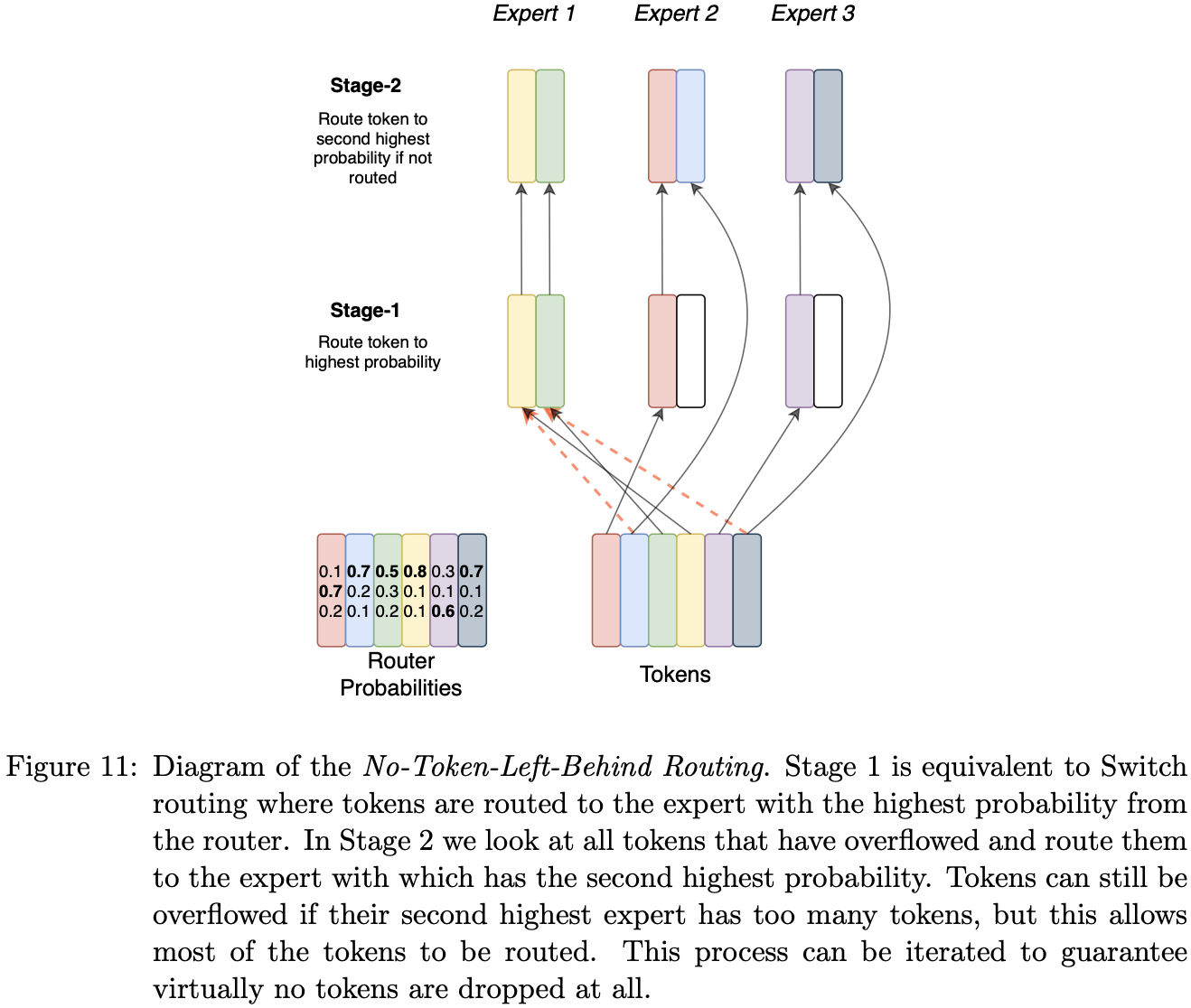
We hypothesised that this could improve performance and further stabilize training, but we found no empirical benefits. We suspect that once the network learns associations between different tokens and experts, if this association is changed (e.g. sending a token to its second highest expert) then performance could be degraded.

switch_transformers, page 29

New load balancing loss

Switch Transformers simplifies the original design in Shazeer et al. (2017) which had separate load-balancing and importance-weighting losses.

switch_transformers, page 7

Given $N$ experts indexed by $i=1$ to $N$ and a batch $\mathcal{B}$ with $T$ tokens, the loss is calculated as follows:

$$\begin{array}{rl}\text{loss}& =\alpha \cdot N\cdot \sum _{i=1}^N{f}_i\cdot P_i\\ f_i& =\frac{1}{T}\sum _{x\in \mathcal{B}}1\{\text{argmax }p(x)=i\}\\ P_i& =\frac{1}{T}\sum _{x\in \mathcal{B}}{p}_i(x)\end{array}$$

Key Definitions:

• $f_i$: The fraction of tokens dispatched to expert $i$.
• $P_i$: The fraction of the router probability allocated for expert $i$.
• Objective: The loss is minimized when both $f$ and $P$ have values of $1/N$, encouraging a uniform distribution.

The objective can also be differentiated as $P$-vector is differentiable, but the $f$-vector is not.

throughout this work we use an $\alpha =10^{-2}$ which was sufficiently large to ensure load balancing while small enough to not to overwhelm the primary cross-entropy objective.

switch_transformers, page 8

Make it stabler

• Selective precision: use fp32 within router and bf16 in other parts. Make sure only bf16 is in all-to-all operations.
• Smaller parameter initialization:

We initialize our weight matrices by drawing elements from a truncated normal distribution with mean $\mu =0$ and standard deviation $\sigma =\sqrt{s/n}$ where s is a scale hyper-parameter and n is the number of input units in the weight tensor (e.g. fan-in) As an additional remedy to the instability, we recommend reducing the default Transformer initialization scale s = 1.0 by a factor of 10.

switch_transformers, page 10

Dropout when fine tuning

They pretrain on a large corpus followed by fine-tuning on smaller downstream tasks. Smaller dataset leads to overfitting.

We thus propose a simple way to alleviate this issue during fine-tuning: increase the dropout inside the experts, which we name as expert dropout. During fine-tuning we simply increase the dropout rate by a significant amount only at the interim feed-forward computation at each expert layer.

switch_transformers, page 11

However, setting a smaller dropout rate (0.1) at non-expert layers and a much larger dropout rate (0.4) at expert layers leads to performance improvements on four smaller downstream tasks

switch_transformers, page 11

It trains fast

Our Switch-Base 64 expert model achieves the same performance of the T5-Base model at step 60k at step 450k, which is a 7.5x speedup in terms of step time.

switch_transformers, page 12

Later they got 7x training time speed up too. This basically means the communication cost is not high.

Distillation

They tried distilling to a dense model with the same FLOP matched dense model. So inference speed is the same, but model size much smaller.

Technique	Parameters	Quality (↑)
T5-Base	223M	-1.636
Switch-Base	3,800M	-1.444
Distillation	223M	(3%) -1.631
+ Init. non-expert weights from teacher	223M	(20%) -1.598
+ 0.75 mix of hard and soft loss	223M	(29%) -1.580
Initialization Baseline (no distillation)
Init. non-expert weights from teacher	223M	-1.639

Parallelism

This is before the time that we have tensor parallelism, pipeline parallelism etc., back when the model and the infra improvement can be in the same paper.

For the “model parallelism” here, they are splitting the FFN layer between devices. They tuned how do balance the splitting.

Limitations

The training is not stable for large models.

While our stability techniques were effective for our Switch-Base, Switch-Large and Switch-C models (no observed instability), they were not sufficient for Switch-XXL.

switch_transformers, page 26

As a result, though this is our better model on a step-basis, we do not pre-train for a full 1M steps, in-line with the final reported results of T5

switch_transformers, page 23

Downstream tasks may have worse performance

Generally we find that improved pre-training quality leads to better downstream results (Appendix E), though we sometimes encounter striking anomalies.

switch_transformers, page 26

We note that while the SwitchXXL has state-of-the-art Neg. Log Perp. on the upstream pre-training task, its gains have not yet fully translated to SOTA downstream performance.

switch_transformers, page 24

This warrants future investigation and study to fully realize the potential of sparse models. Understanding the fine-tuning dynamics with expert-models is very complicated and is dependent on regularization, load-balancing, and fine-tuning hyper-parameters.

switch_transformers, page 32

Apply MoE to self attention leads to training instabilities.

In Appendix A, we report quality improvement adding these inside Self-Attention layers, where our layer replaces the weight matrices which produce Q, K, V. However, due to training instabilities with the bfloat16 format, we instead leave this as an area for future work.

switch_transformers, page 27