To really understand what’s going on, see Andrej’s Neural Networks: Zero to Hero lecture. Specifically, Lecture 7: Lecture 7: Let’s build GPT: from scratch, in code, spelled out. Obviously GPT-2 is basically this, but using a lot of data.
Input, output and loss
Suppose we use the very basic character tokenizer, that maps every letter / symbol into some int.
batch_size = 4 # how many independent sequences will we process in parallel? B
block_size = 8 # what is the maximum context length for predictions? TThen the x and y (batched) would both have shape of (B, T), like this:
inputs:
torch.Size([4, 8])
tensor([[24, 43, 58, 5, 57, 1, 46, 43],
[44, 53, 56, 1, 58, 46, 39, 58],
[52, 58, 1, 58, 46, 39, 58, 1],
[25, 17, 27, 10, 0, 21, 1, 54]])
targets:
torch.Size([4, 8])
tensor([[43, 58, 5, 57, 1, 46, 43, 39],
[53, 56, 1, 58, 46, 39, 58, 1],
[58, 1, 58, 46, 39, 58, 1, 46],
[17, 27, 10, 0, 21, 1, 54, 39]])
Targets is basically input, shifted by one. In each of this samples there are actually T samples for each “item”:
when input is [24] the target: 43
when input is [24, 43] the target: 58
when input is [24, 43, 58] the target: 5
when input is [24, 43, 58, 5] the target: 57
This is enforced by the loss function:
logits = logits.view(B*T, C)
targets = targets.view(B*T)
# For each batch and time, there's a corresponding expected output.
# There's mechanism in decoder-only self attention to make sure output for [24] only look at [24].
loss = F.cross_entropy(logits, targets)Generation
One important aspect of transformer is that its parameter does not depend on T (context length). So you can start from one char, and then keep appending new result to the input and ask the network what’s the output. For a t size sequence, network also output t size output, we only need the last one here.
def generate(self, idx, max_new_tokens):
# idx is (B, T) array of indices in the current context
for _ in range(max_new_tokens):
# crop idx to the last block_size tokens
idx_cond = idx[:, -block_size:]
# get the predictions
logits, loss = self(idx_cond)
# focus only on the last time step
logits = logits[:, -1, :] # becomes (B, C)
# apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (B, C)
# sample from the distribution
idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
# append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idxBuilding self attention
Let’s pay attention (pun not intended) for the very basic formula:
Think about the following questions:
- What’s
softmaxdoing here? - What if we want each token to only attend to stuff before it? (This paper is machine translation so it does not matter)
- What about that ?
Andrej’s interpretation:
- Matrix multiplication is weight aggregation.
# toy example illustrating how matrix multiplication can be used for a "weighted aggregation"
torch.manual_seed(42)
a = torch.tril(torch.ones(3, 3))
a = a / torch.sum(a, 1, keepdim=True)
b = torch.randint(0,10,(3,2)).float()
c = a @ ba= tensor([[1.0000, 0.0000, 0.0000],
. [0.5000, 0.5000, 0.0000],
[0.3333, 0.3333, 0.3333]])
--
b= tensor([[2., 7.],
[6., 4.],
[6., 5.]])
--
c= tensor([[2.0000, 7.0000],
[4.0000, 5.5000],
[4.6667, 5.3333]])
Here this c is “mean of the first n tokens.” Assuming the b is of size TxC, we are basically computing for all context lengths.
Using softmax there is just convenient way of creating weights between to do this aggregation. Self attention make this weight learnable.
# version 4: self-attention!
torch.manual_seed(1337)
B,T,C = 4,8,32 # batch, time, channels
x = torch.randn(B,T,C)
# let's see a single Head perform self-attention
head_size = 16
key = nn.Linear(C, head_size, bias=False)
query = nn.Linear(C, head_size, bias=False)
value = nn.Linear(C, head_size, bias=False)
k = key(x) # (B, T, 16)
q = query(x) # (B, T, 16)
wei = q @ k.transpose(-2, -1) # (B, T, 16) @ (B, 16, T) ---> (B, T, T)
tril = torch.tril(torch.ones(T, T))
#wei = torch.zeros((T,T))
wei = wei.masked_fill(tril == 0, float('-inf'))
wei = F.softmax(wei, dim=-1)
v = value(x)
out = wei @ v
#out = wei @ xFor that scaled part, since we’re doing q@k there, if the inputs are all unit gaussian, wei’s distribution would be , thus making the softmax too sharp, converge to max.
Multi-head attention
class MultiHeadAttention(nn.Module):
""" multiple heads of self-attention in parallel """
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
self.proj = nn.Linear(n_embd, n_embd)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
out = torch.cat([h(x) for h in self.heads], dim=-1)
out = self.dropout(self.proj(out))
return outDon’t forget linear layers
See that feed forward part in the diagrams? They are needed. Attention focus on “getting info from other times”, or communication. Feed forward layers mixes up the C channel, or think.
More tricks
- To make the network able to handle large amount of data, we need regularization, which is done by
- LayerNorm, which is basically does norm in “input params” instead of in batch. So it doesn’t need to distinguish train / eval as there’s no running mean.
- Skip connection.
- Add dropout
Encoder / decoder / only
The left part of the diagram is encoder, the other is decoder. If you operate on the same domain for input and output, you can do decoder only.
My original notes for the paper
- The use of self attention inside both encoder and decoder itself, not only encoder-decoder level “normal” attention
- The clever positional encoding with sin and cos waves, and use residual blocks to propagate that information. You can think of it as a more concise way of binary encoding (for floats).
Transformer Architecture: The Positional Encoding
- Multi-head attention is kinda like general attention where a linear layer is used when combining key and query, but probably better, as we could have multiple key, value, query now.
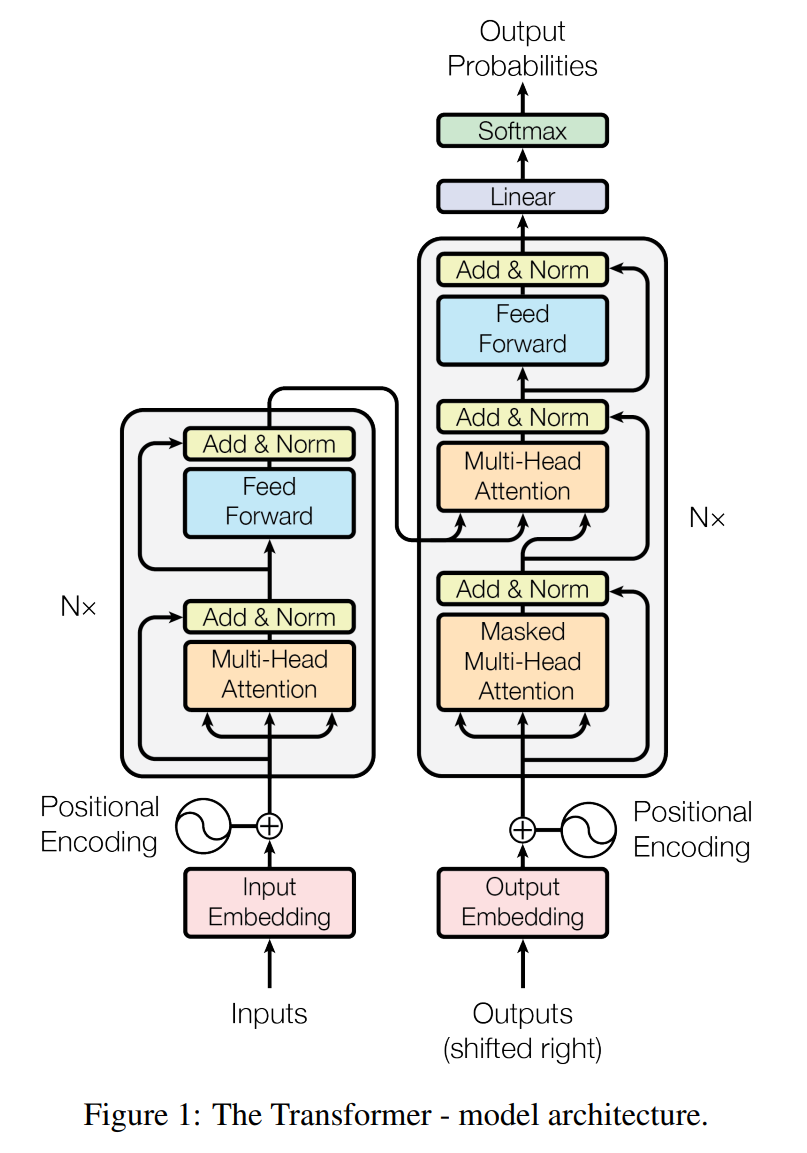
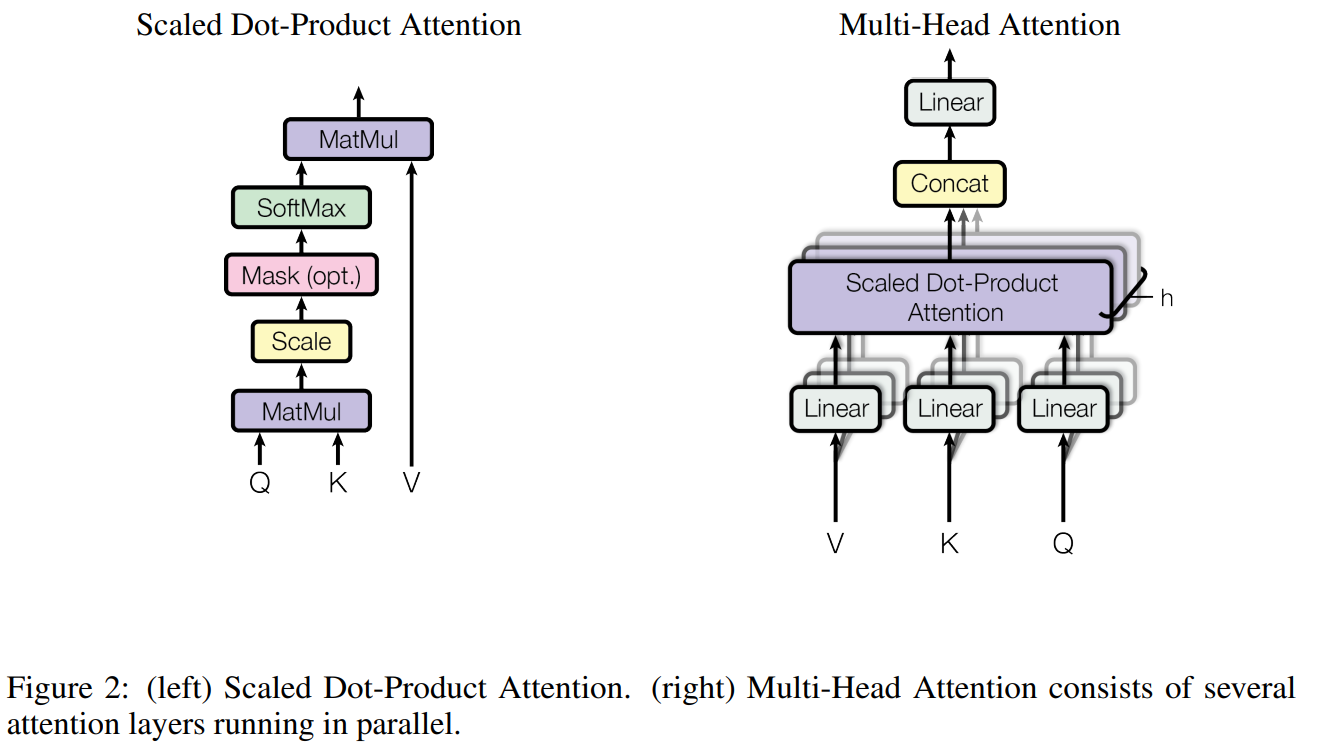
The OG transformer uses Absolute position embedding.