Mixture of Experts

MoE is a general idea, but we are focusing on the first mainstream paper here. For an overview, see Mixture of Experts Overview.

Note the first Author is Noam Shazeer and the last author is Geoffrey Hinton with Jeff Dean. You know this is gonna be a great paper.

The promise: conditional computation, so we can increase model capacity without a proportional increase in computational costs. The design choices are to solve the following challenges:

GPUs are slow at branching.
Batch size need to be big for good performance
Network bandwidth can be a bottleneck. The ideal case is to let compute demand vs network demand match that of the capability.
Loss terms need to be carefully designed for regularization
Small model

As this is a 2017 papers, the base model is stacked LSTM. The MoE layer is in between LSTM layers, called once for each position in the text.

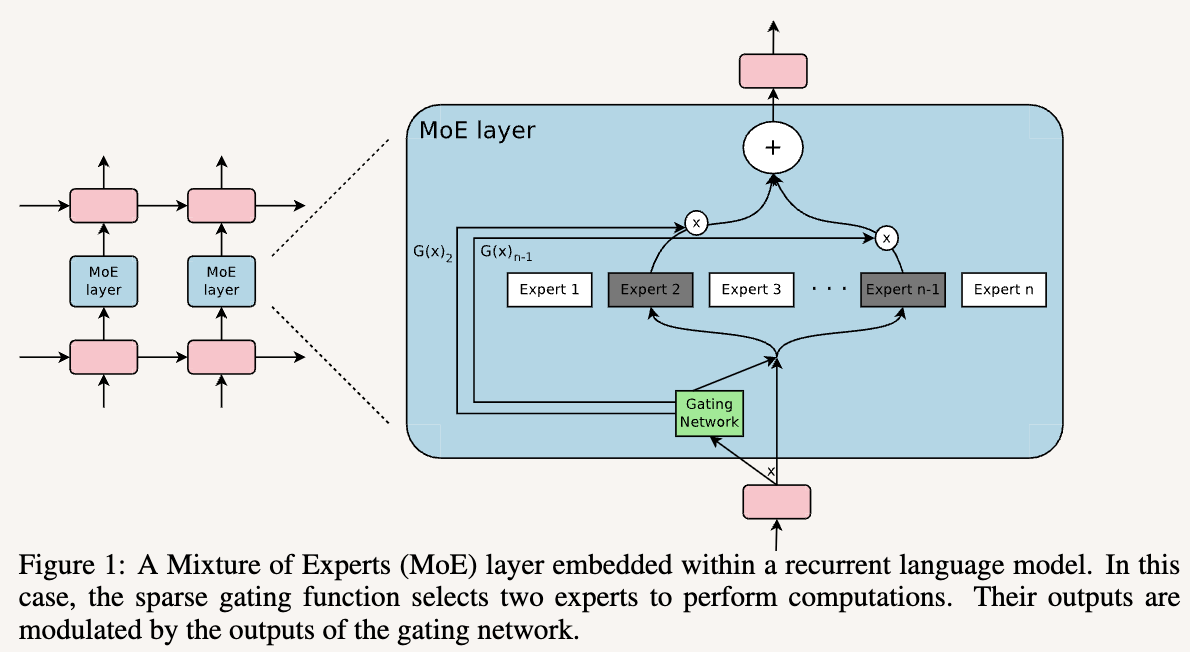
The structure of MoE layers

There are $n$ expert networks $E_{1,} \dots E_{n}$ , and a gating network $G$ . $G$ outputs a sparse $n$ -dimensional vector. We select top k from that vector and adds the output of the selected expert together. That’s it.

Let us denote the output of these networks $E_{i} (x)$ and $G (x)$ , the output $y$ of the MoE module can be written as

y = i = 1 \sum n G (x)_{i} E_{i} (x)

So we basically skip computation of $E_{i} (x)$ whenever that is not selected.

Gating network

Obviously the most simple form is just linear layer followed by Softmax. On top of that they added sparsity and noise.

G (x) H (x)_{i} Kee pT o p K (v, k)_{i} = S o f t ma x (Kee pT o p K (H (x), k)) = (x \cdot W_{g})_{i} + St an d a r d N or ma l () \cdot S o f tpl u s ((x \cdot W_{n o i se})_{i}) = {v_{i} - \infty if v_{i} is in the top k elements of v . otherwise.

You can see the KeepTopKoperation is done before Softmax. We can also do it after softmax and then re-normalize, same thing (see Appendix F).

That Gaussian noise and $W_{n o i se}$ is there so it’s now “soft” topk. We’ll discuss it more in the loss section.

Get large batch size

Data + model parallelism

Shard the MoE layer by expert. Each device has full other layers + only a subset of the experts.

Data flows like this:

All devices process their own data through the initial data-parallel layers (like the first LSTM).
The gating network on each device decides which experts are needed for its local examples.
The Combination Step: The relevant examples from all devices are sent across the network to the specific device that hosts the required expert.
Each expert processes a “combined batch” consisting of all relevant examples from the entire cluster.
The results are then sent back to the original devices to continue through the rest of the data-parallel layers.

Quite some network.

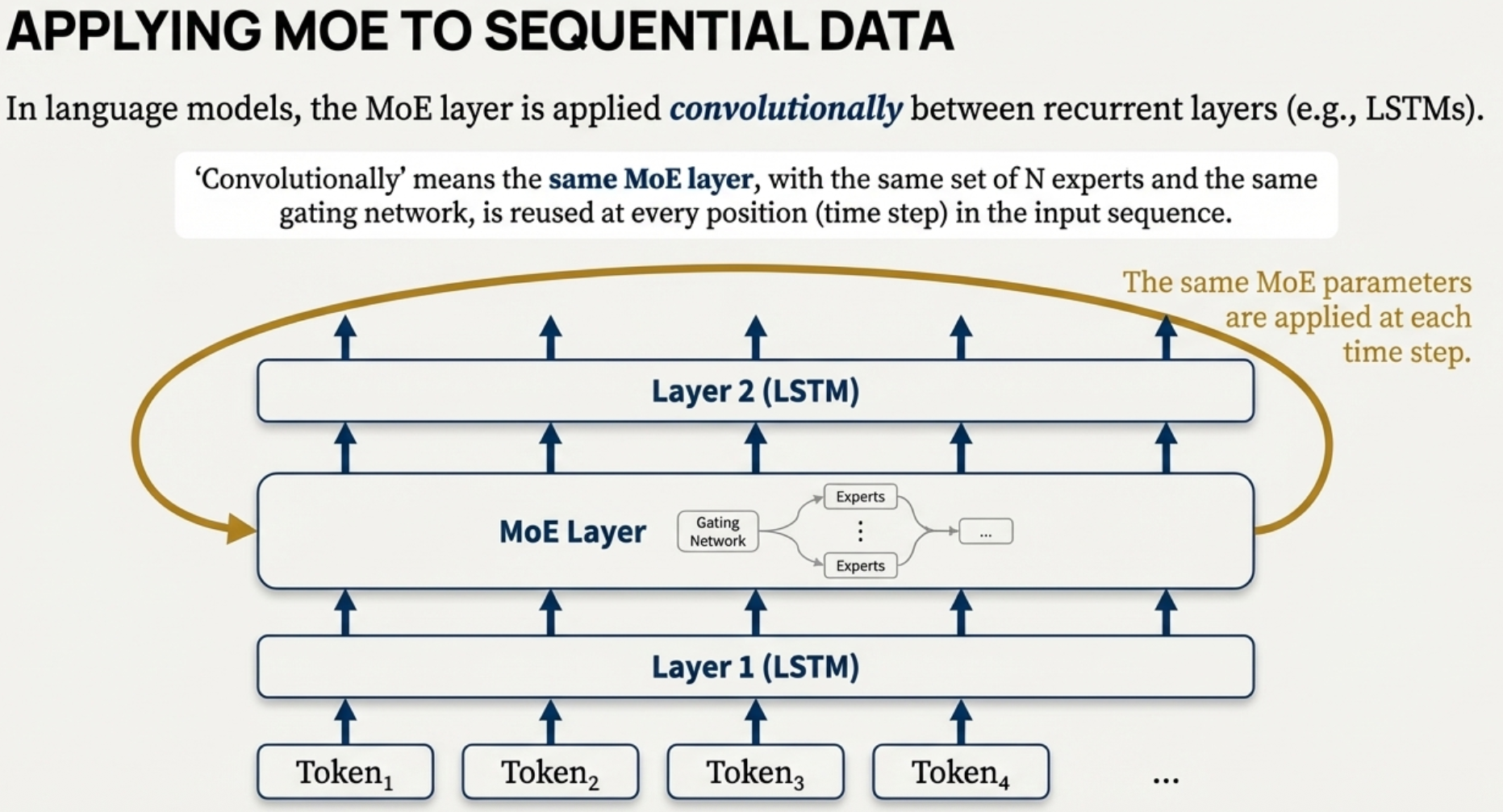
Convolutionality

RNNs are sequential, the MoE layers are not. So we can run the first LSTM layer, get the full result, then pass it as a big batch to MoE, get result, then run the second LSTM layer.

Loss

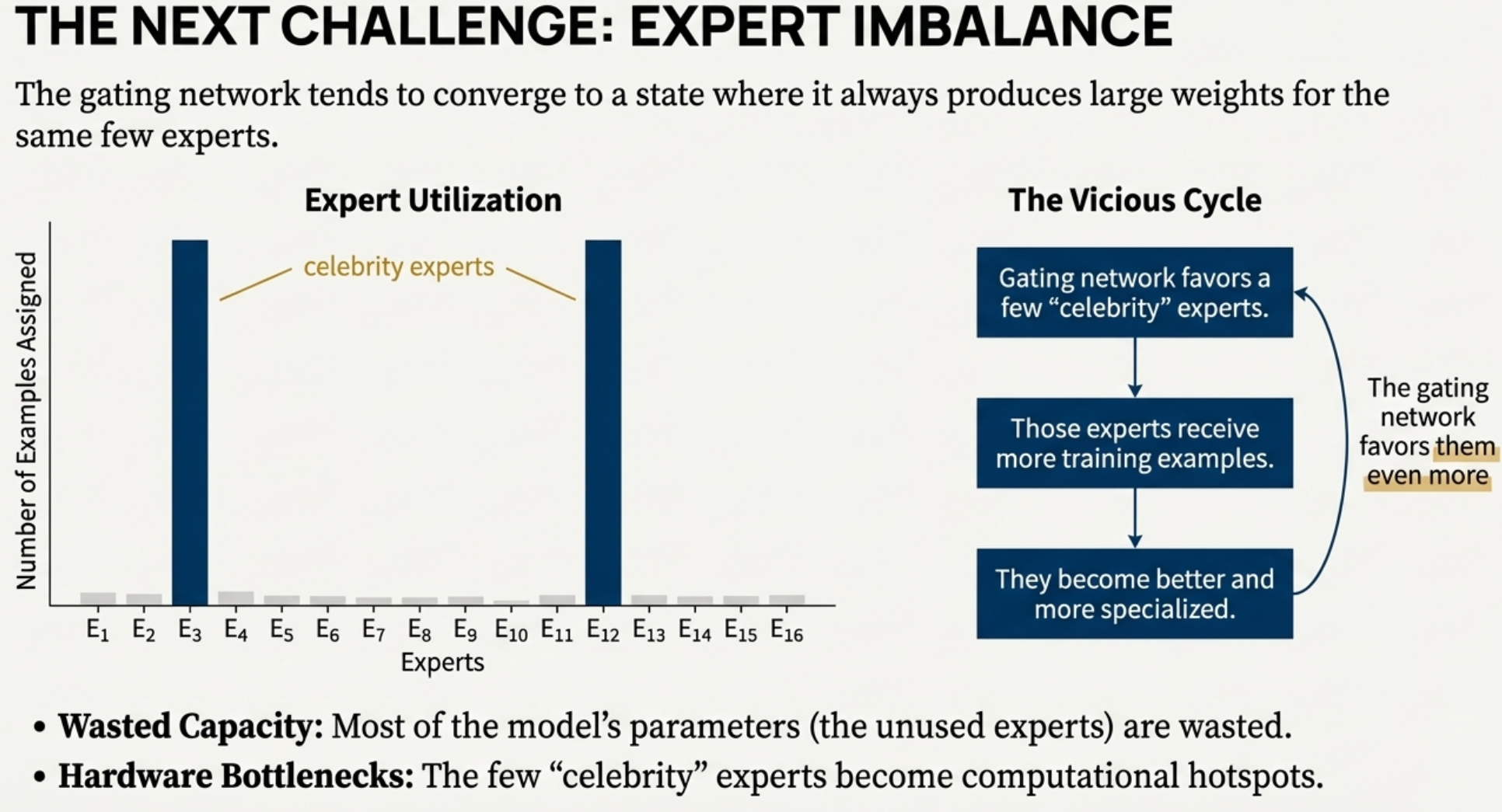
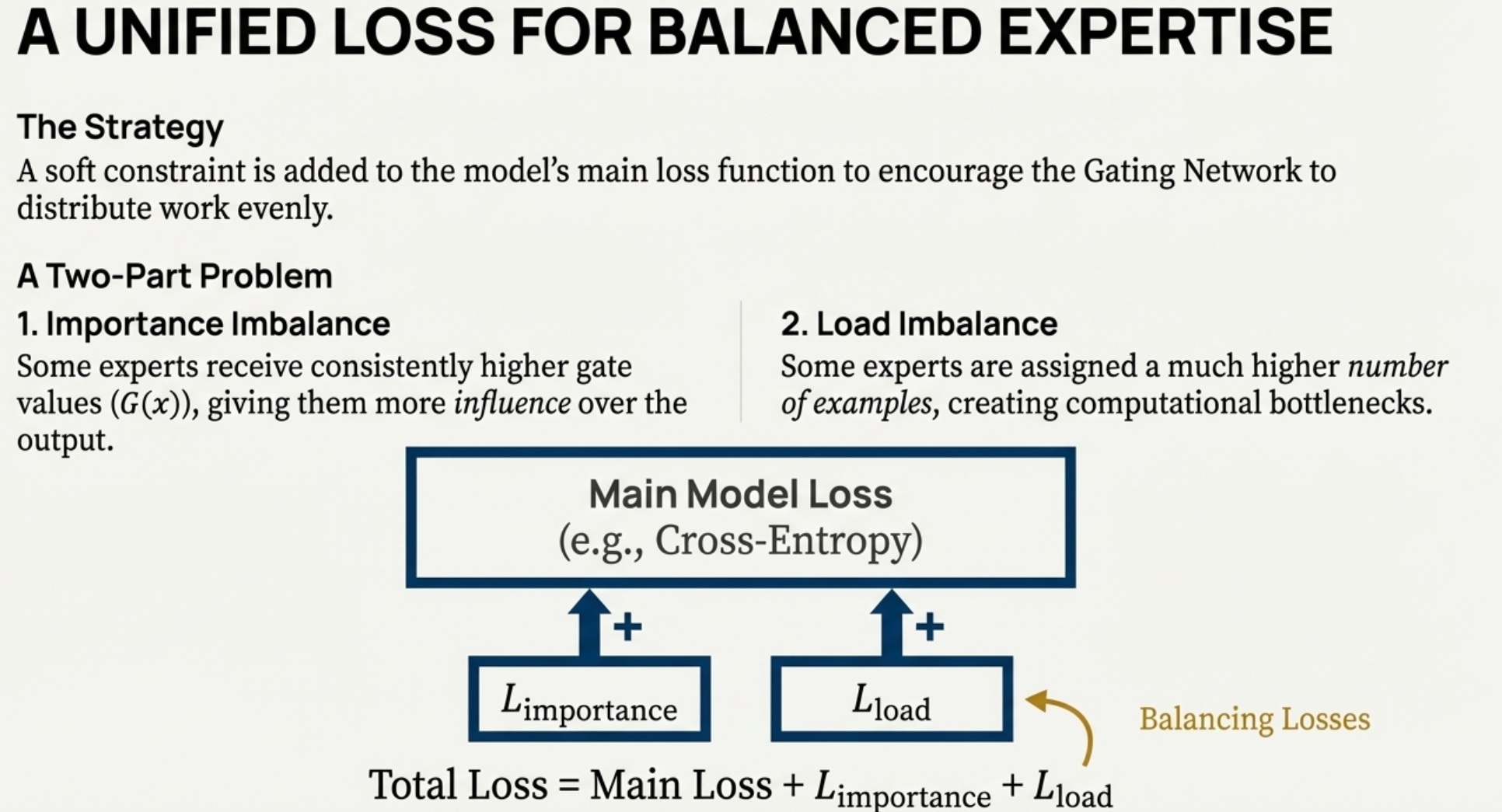
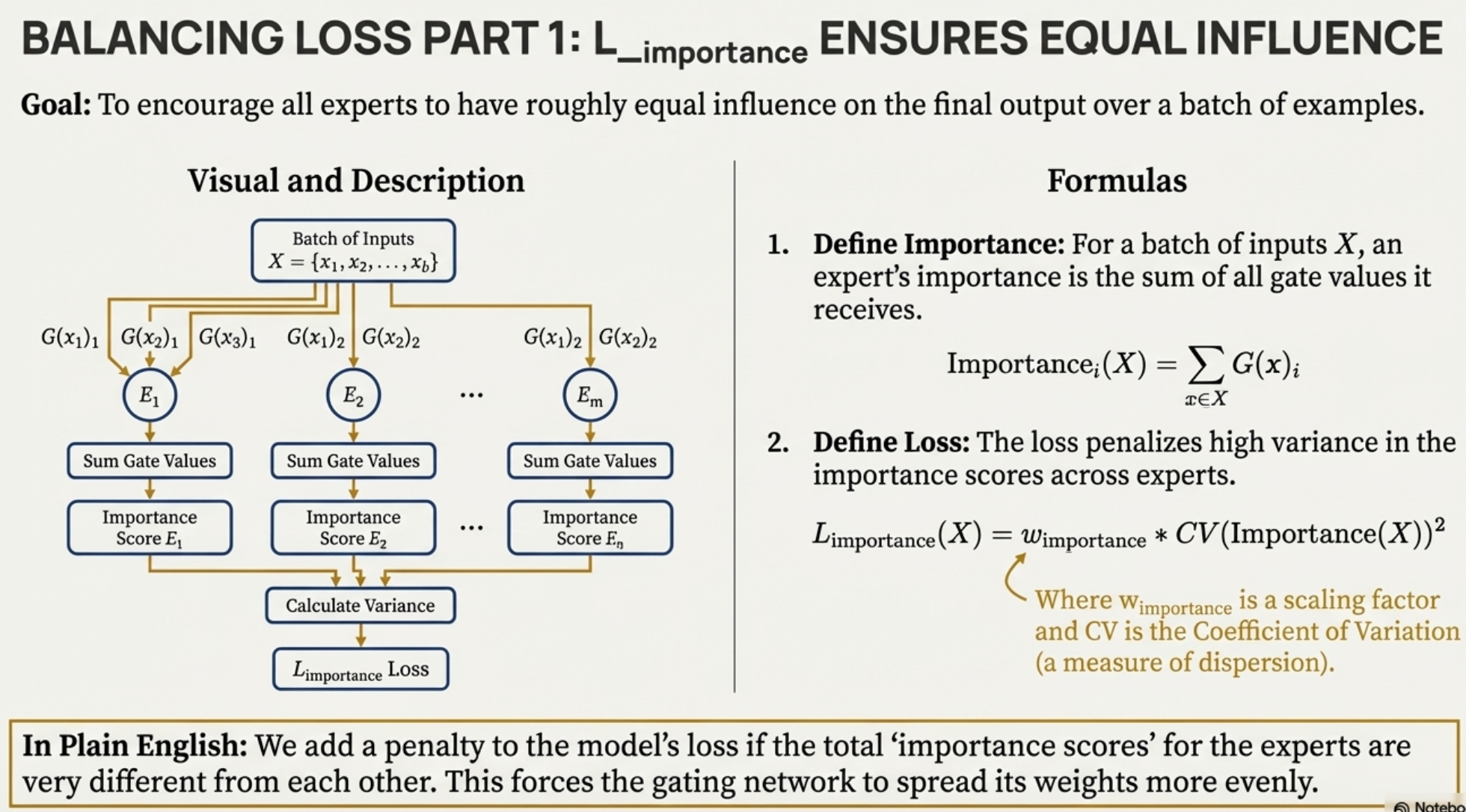
So say we want to do back prop, since there’s this hard discrete top k, we’ll only update the weights for these. How do we enforce that the load is load balanced well?

for load-balancing purposes, we want to define an additional loss function to encourage experts to receive roughly equal numbers of training examples. Unfortunately, the number of examples received by an expert is a discrete quantity, so it can not be used in backpropagation.

moe, page 13

Via a trick, we can convert this hard count problem into a soft probability problem.

Instead, we define a smooth estimator Load(X) of the number of examples assigned to each expert for a batch X of inputs.

moe, page 13

This zero-mean, fuzzy setup means that topk now becomes a soft topk, with tunable parameter for how uncertain it is in different locations.

Give me some number

4, 32 or 256 is used for flat experts. 256 to 131072 experts are used for hierarchical MoEs (MoE routes to MoE).

For 8M-ops model,

Layer Type	Parameters (Approx)	Computation (Ops/Timestep)
Two LSTMs	~4–9 Million	4 Million
MoE Layer	Up to 137 Billion	4 Million (for $k = 4$ )

Yanda's Random Notes

Explorer