One would be surprised that I’ve never read ResNet paper till recently. It turns out the paper contains more information than the simple residual shortcut.
Inspiration
ResNet aims to solve a mysterious problem that the optimizer is not able to find optimal weights for deep networks:
When deeper networks are able to start converging, a degradation problem has been exposed: with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error
We argue that this optimization difficulty is unlikely to be caused by vanishing gradients. These plain networks are trained with BN, which ensures forward propagated signals to have non-zero variances. We also verify that the backward propagated gradients exhibit healthy norms with BN. So neither forward nor backward signals vanish. In fact, the 34-layer plain net is still able to achieve competitive accuracy (Table 3), suggesting that the solver works to some extent. We conjecture that the deep plain nets may have exponentially low convergence rates, which impact the reducing of the training error3. The reason for such optimization difficulties will be studied in the future
Anyway, they charge ahead and propose let the network learn a easier thing: the residual mapping to the original input.
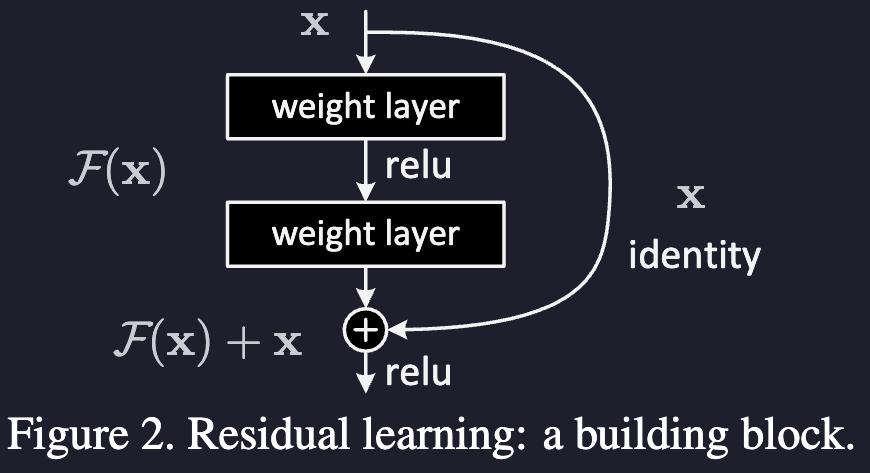
The dimensions of x and F must be equal in Eqn.(1). If this is not the case (e.g., when changing the input/output channels), we can perform a linear projection Ws by the shortcut connections to match the dimensions:
Small design choices
There is [ablation study](resnet, page 6) that shows even though we can replace that identity connection is enough.
The paper author also [prefers](resnet, page 3) to have multiple layers inside the residual blocks.
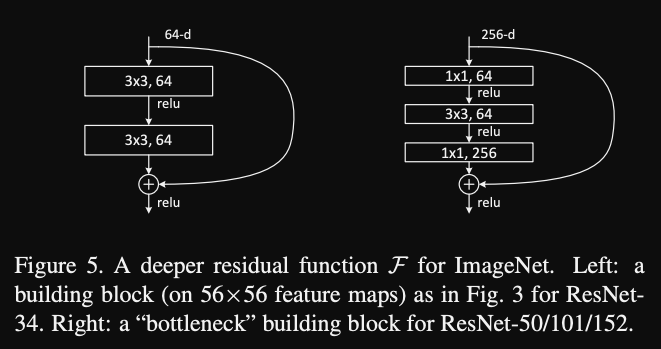
Bottleneck block
For deeper 50+ layer network, a bottleneck block is used for training time concerns. It’s claimed that the change have similar time complexity.
]
Residual Networks Behave Like Ensembles of Relatively Shallow Networks
To understand why ResNet works so well, quite some paper reference this one, even ResNext.
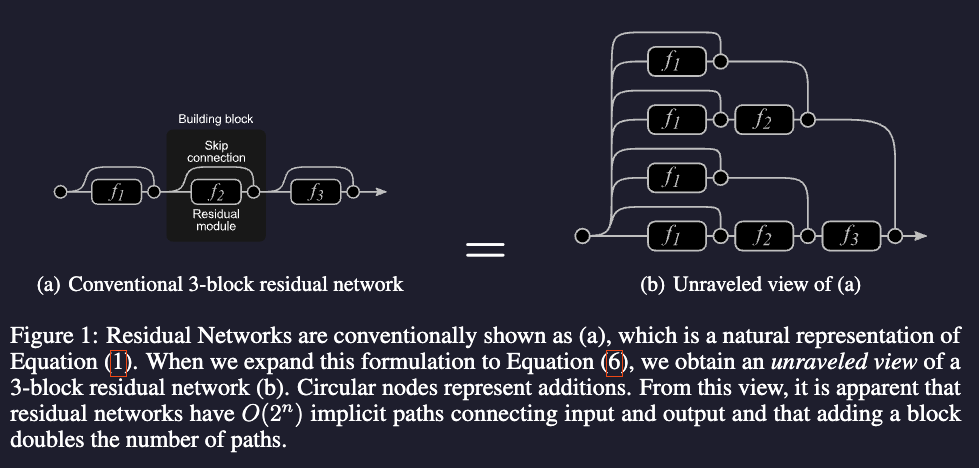
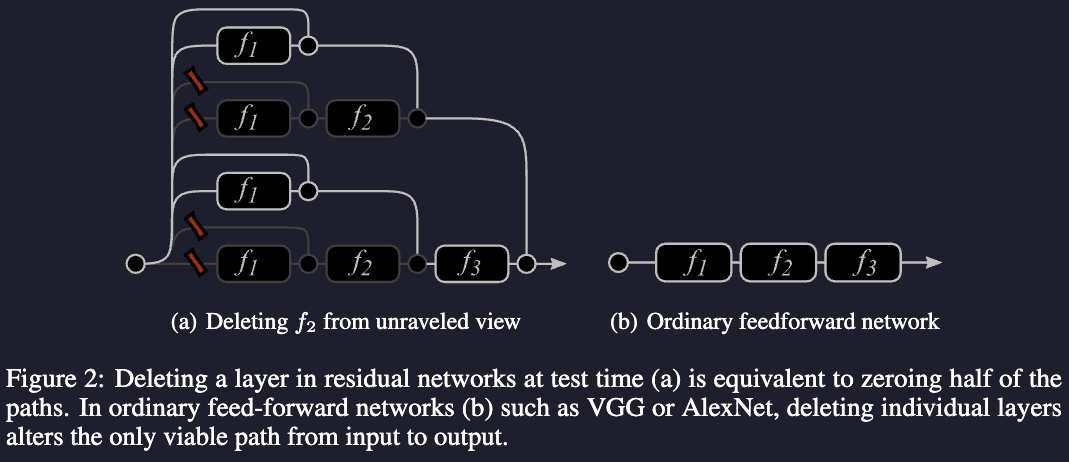This can explain why we can delete layers from ResNet and the performance is not decreased much (we are just reducing the number of paths), why this property cannot hold for more traditional networks. We can even reorder the modules.
From that interpretation we can know which paths are the important ones.
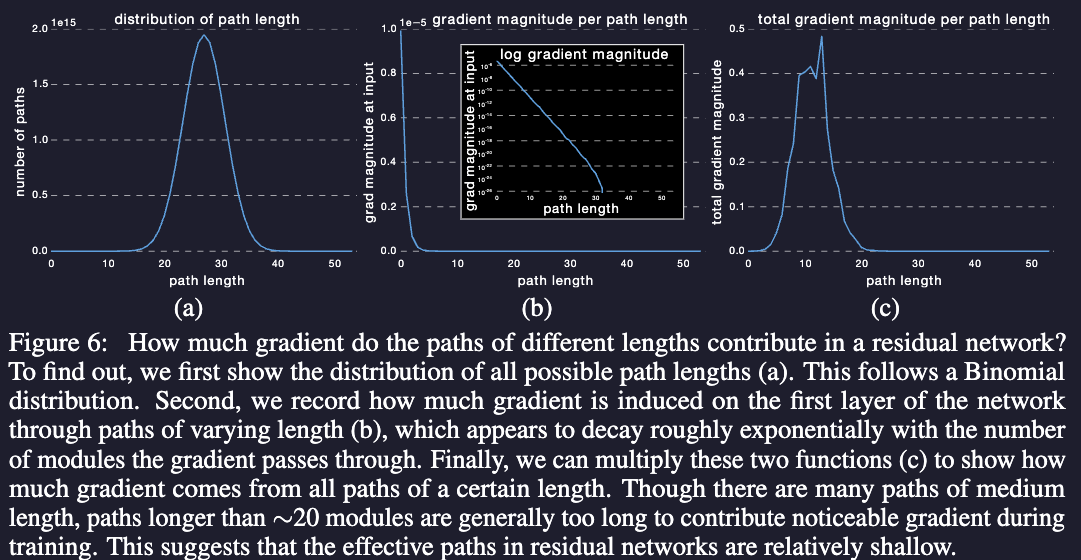
The effective paths in residual networks are relatively shallow Surprisingly, almost all of the gradient updates during training come from paths between 5 and 17 modules long. These are the effective paths, even though they constitute only 0.45% of all paths through this network. Moreover, in comparison to the total length of the network, the effective paths are relatively shallow.