Another paper with Jian Sun as the corresponding Author, who also contributed to ShuffleNet series and ResNet. This is also the most well known structure-parameterization paper. For other ones see Xiaohan’s homepage.
The network follows all the guidelines in ShuffleNet V2. Specifically, it has a VGG-like plain topology, no branches, only conv and ReLU. No Depthwise Separable Convolution. So even if it has high FLOPs number, it actually runs faster than e.g. EfficientNet. A detailed reasoning can be found at Simple is Fast, Memory-economical, Flexible.
Since the multi-branch topology has drawbacks for inference but the branches seem beneficial to training, we use multiple branches to make an only-training-time ensemble of numerous models.
Another trick that makes it fast is Winograd convolution, which is a special algorithm only on conv with stride . With benchmark it’s obvious is the superior one. Note that the algorithm may be selected in PyTorch with torch.backends.cudnn.benchmark = True. It’s essentially trading FLOP with memory access, so whether it’s really faster depends on the input and hardware.

The core of structure parameterization is this:
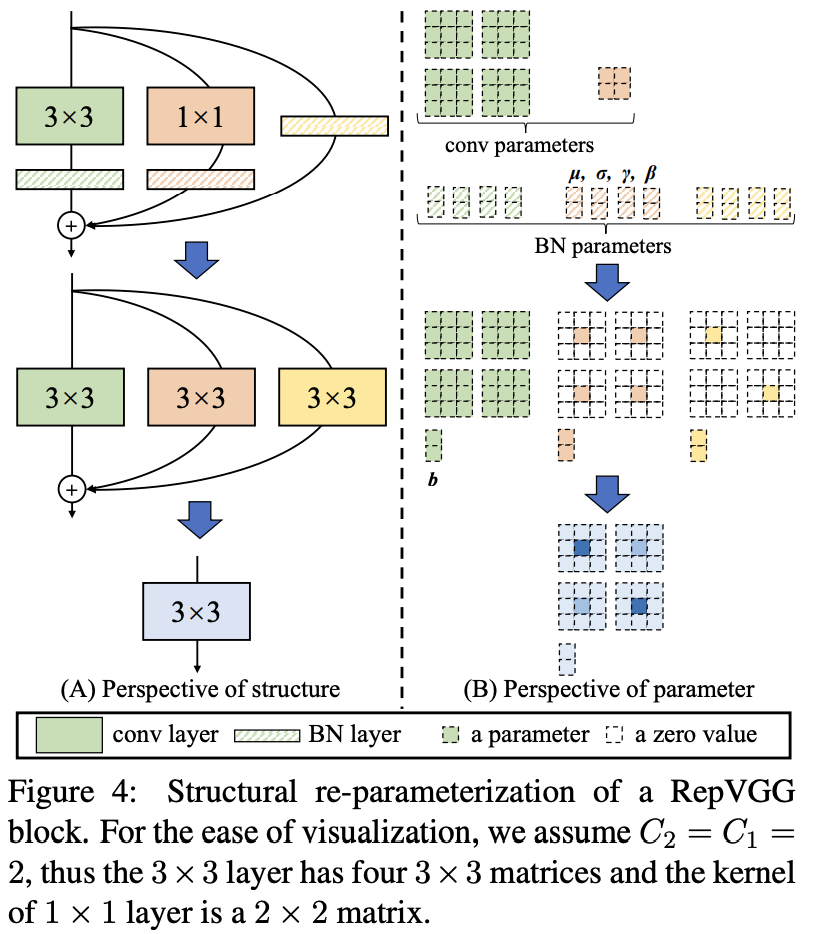
- We can fold BN directly to convolution layer (which is common optimization nowadays).
- convolution can be viewed as convolution with only center param.
- Identity branch is a special case of convolution, where there are no cross-channel information. That’s the reason you see the identity metrics-like param there.
Since it’s all linear system, adding result of together is just adding and together. Note there’s BN here for each branch, so it’s not “trivial re-parameterization”. The network is learning nonlinear stuff in training time, instead of just a different representation of conv kernels. This would not work if there is ReLU for each branch.
We reckon the superiority of structural re-param over DiractNet and Trivial Re-param lies in the fact that the former relies on the actual dataflow through a concrete structure with nonlinear behavior (BN), while the latter merely uses another mathematical expression of conv kernels. The former “re-param” means “using the params of a structure to parameterize another structure”, but the latter means “computing the params first with another set of params, then using them for other computations”. With nonlinear components like a training-time BN, the former cannot be approximated by the latter.
For Network design:
We decide the numbers of layers of each stage follow- ing three simple guidelines.
- The first stage operates with large resolution, which is time-consuming, so we use only one layer for lower latency.
- The last stage shall have more channels, so we use only one layer to save the parameters.
- We put the most layers into the second last stage (with 14 × 14 output resolution on ImageNet), following ResNet and its recent variants [12, 28, 38] (e.g., ResNet-101 uses 69 layers in its 14 × 14-resolution stage). We let the five stages have 1, 2, 4, 14, 1 layers respectively to construct an instance named RepVGG-A. We also build a deeper RepVGG-B, which has 2 more layers in stage2, 3 and 4. We use RepVGG-A to compete against other lightweight and middleweight models including ResNet-18/34/50, and RepVGG-B against the high-performance ones.
Through their experiment, this is pretty good, but not so different from ResNet. Better results may come from with same speed, RepVGG is able to pack in more FLOPs.
suggesting that RepVGG- style structural re-parameterization is not a generic over- parameterization technique, but a methodology critical for training powerful plain ConvNets.