DINO

Summary

DINO is a ViT based self supervised learning approach without Contrastive learning. It uses with no labels for achieving that. 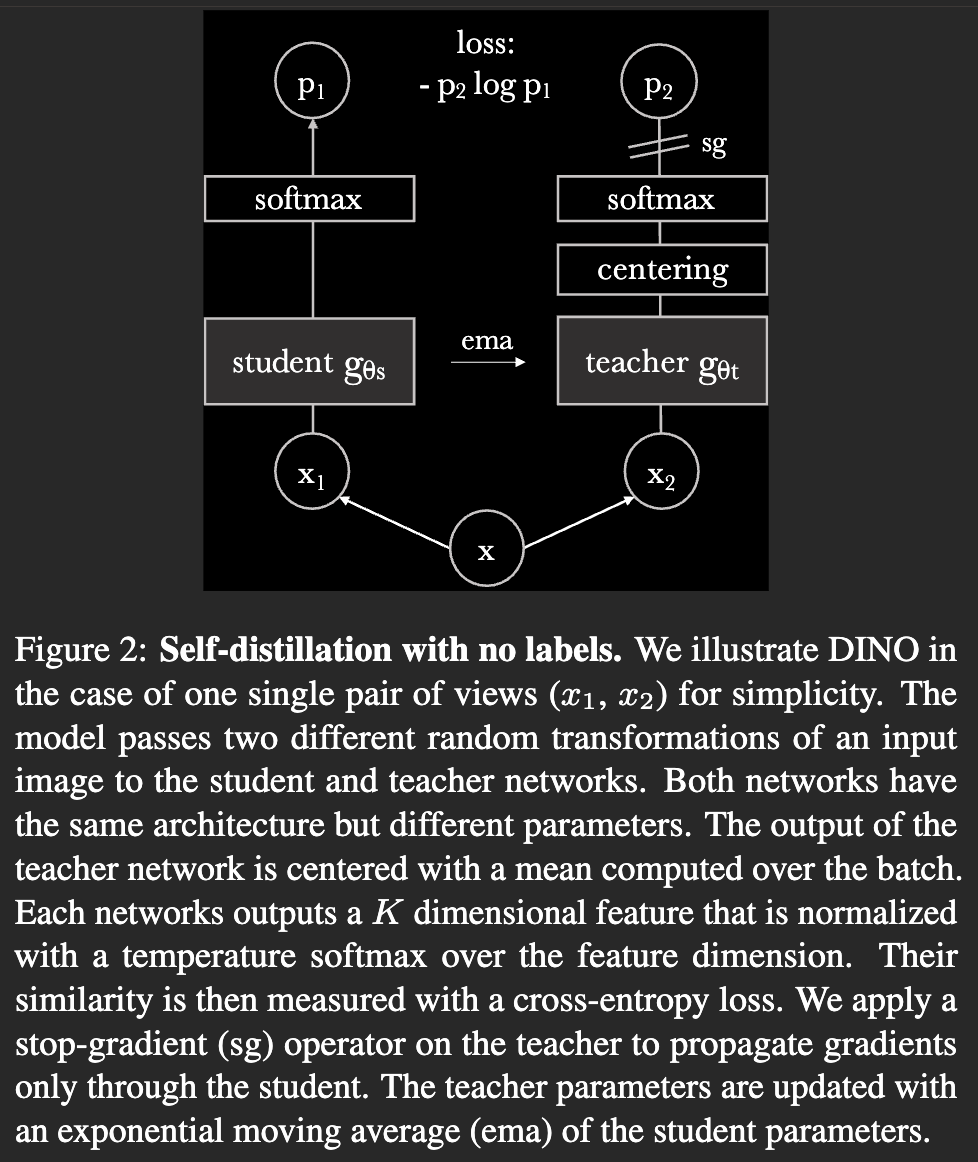This image basically summaries it all. We only train student network, and then update the teacher network with exponential mean average. This momentum encoder is adapted from MoCo, and the Mean Teacher self-distillation part is inspired from BYOL.

We propose to interpret the momentum teacher in DINO as a form of Polyak-Ruppert averaging with an exponentially decay. dino, page 9

Details

More precisely, from a given image, we generate a set V of different views. This set contains two global views, $x_1^g$ and $x_2^g$ and several local views of smaller resolution. All crops are passed through the student while only the global views are passed through the teacher, there- fore encouraging “local-to-global” correspondences.

dino, page 3

One may ask: how does the training not collapse? If you’re asking it to produce the same information on two versions of augmented images, why don’t the model just output the same thing regardless of input? DINO uses two things together:

• Centering: maintaining a moving average of previous prediction, and subtract the mean before computing loss.
• Sharpening: low temperature for softmax.

The centering avoids the collapse induced by a dominant dimension, but encourages an uniform output. Sharpening induces the opposite effect.

dino, page 9

# gs, gt: student and teacher networks 
# C: center (K) 
# tps, tpt: student and teacher temperatures 
# l, m: network and center momentum rates 
gt.params = gs.params 
for x in loader: # load a minibatch x with n samples 
	x1, x2 = augment(x), augment(x) # random views
	
	s1, s2 = gs(x1), gs(x2) # student output n-by-K
	t1, t2 = gt(x1), gt(x2) # teacher output n-by-K
	
	loss = H(t1, s2)/2 + H(t2, s1)/2
	loss.backward() # back-propagate 
	
	# student, teacher and center updates
	update(gs) # SGD 
	gt.params = l*gt.params + (1-l)*gs.params
	C = m*C + (1-m)*cat([t1, t2]).mean(dim=0)
 
def H(t, s):
	t = t.detach() # stop gradient
	s = softmax(s / tps, dim=1)
	t = softmax((t - C) / tpt, dim=1) # center + Sharpening
	return - (t * log(s)).sum(dim=1).mean()