Conformal Prediction

The note is based on the videos tutorials linked in the website.

Motivation

Conformal predictions is a way to “calibrate” any model so that model’s empirical probability output (e.g. softmax scores for a classification model) can be converted to a rigorous uncertainty.

Some examples:

• For classification tasks asking for multiple category outputs, we provide a calibration set containing $n$ samples, and we want the model to output a set such that $\tau (x_{n+1})\subseteq y$ , and

$$P[y_{n+1}\in \tau (x_{n+1})]\ge 1-\alpha$$

. To put in other words, Output a set so we can say with confidence that the probability that the output set contains the ground truth set with probability $1-\alpha$.

• For regression, we want the model to give a confidence interval for the regressed values.

The general algorithm

1. Identify a heuristic notion of uncertainty using the pre-trained model.

2. Define the score function $s(x,y)\in \mathbb{R}$. (Larger scores encode worse agreement between $x$ and $y$.)

3. Compute $\hat{q}$ as the $\frac{\lceil (n+1)(1-\alpha )\rceil }{n}$ quantile of the calibration scores $s_1=s(X_1,Y_1),...,s_n=s(X_n,Y_n)$.

4. Use this quantile to form the prediction sets for new examples:

$$C(X_{\mathrm{test}})=\left\{y:s(X_{\mathrm{test}},y)\le \hat{q}\right\}.$$

Example time: The score function here is “the softmax logits of the correct class”. And then we see in the calibration set: what’s the $0.1$ percentile of that score? Then we can tell for a new sample: if any class score is larger than that $0.1$ percentile, then we include that in the output set. It can be proved that

$$1-\alpha \le P[Y_{n+1}\in \tau (X_{n+1})]\le 1-\alpha +\frac{1}{n+1}$$

, where $n$ is the calibration set size.

Why does it work

There seem to be some bayesian process in play here: we estimate $y|score$ here, given $score|y$. But no, it’s actually based off the concept of exchangeability, so that it’s not depending on actual data distribution. Not the score is $s(x,y)$, not $s(x)$.

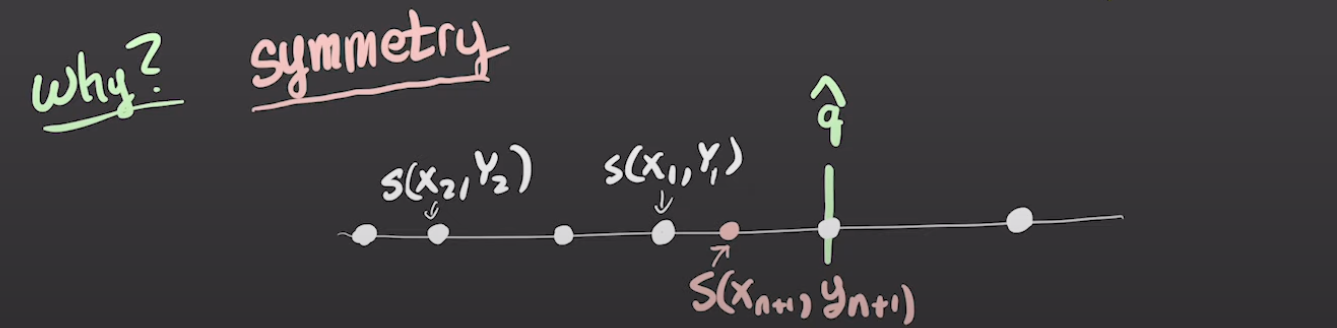
Think about it like this: say the white dots are the calibration samples. Red is the test data. We’ll put $y_{n+1}$ in the output if $s(x_{n+1},y_{n+1})<\hat{q}$. This is right if there’s a “label” $(x_{n+1},{\hat{y}}_{n+1})$ in the calibration set that have a score $<\hat{q}$. Note: we do not care about false positives here. So as long as the score of this “label” actually does not fall on the right side of $\hat{q}$, all is good, and that probability of mistake is $1-\alpha$ (this sample can be between any samples in the calibration set).

Another classification algorithm

Now we use cumulative sum up to the ground truth class as score.

Conformalized quantile regression

First, train models that output quantile values directly. That can be done with Pinball loss. Then you calibrate that quantile:

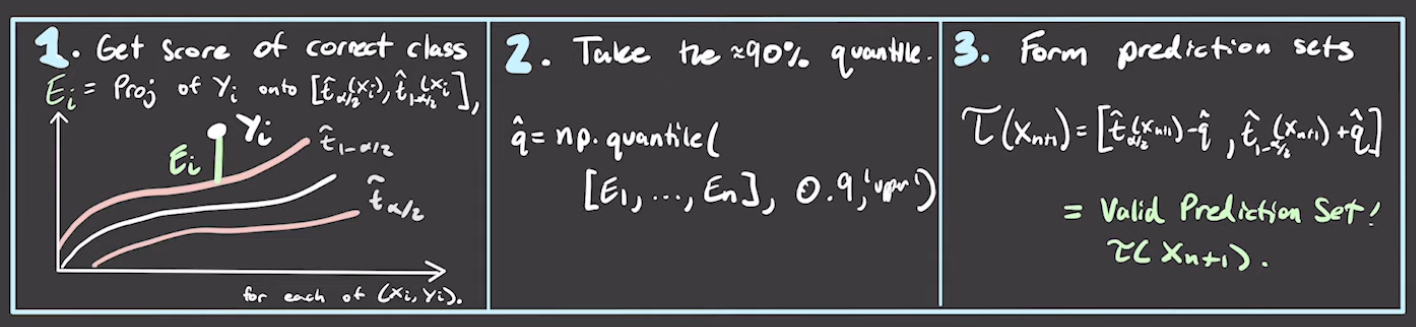
There’s also part 2 and 3 video that I also finished, but didn’t got the time to finish the notes. To be finished later.