DeiT

There are two things covered in the paper:

1. Train a ViT fast and data efficient. This is done mostly through hyperparameter change and data augmentation method.
2. A unique way to distill model and the result model is even better than the teacher.

DeiT, the reference model

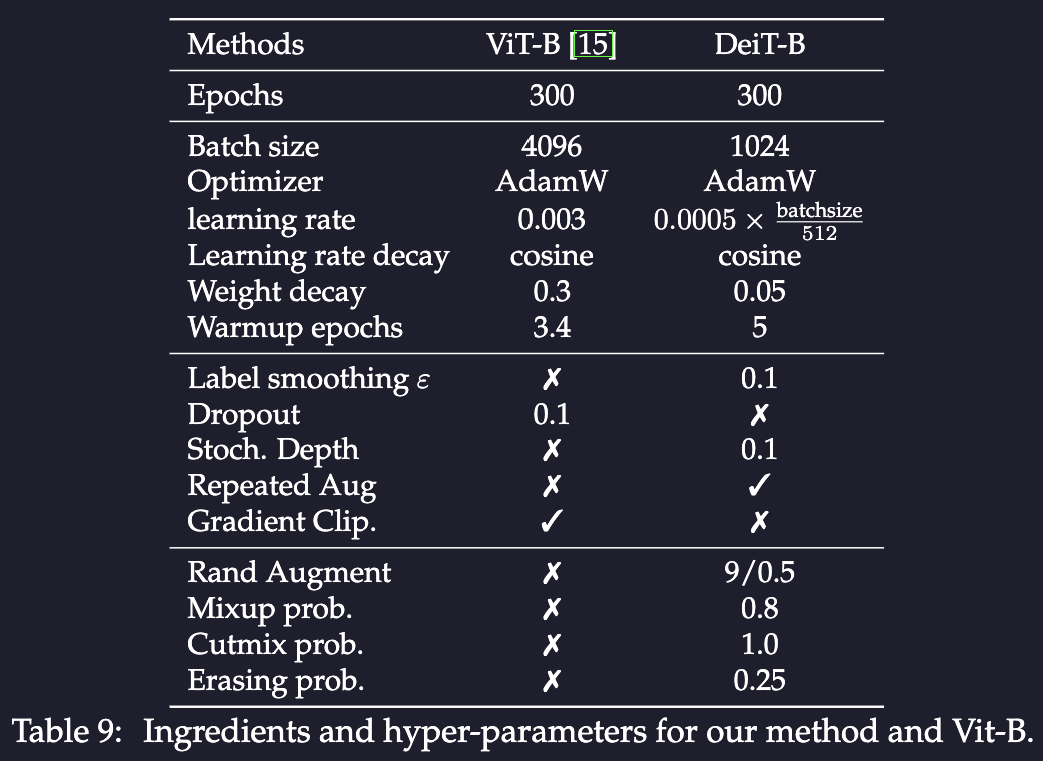
• Truncated normal for initialization. Some option may not converge. This is the recommendation from Hanin and Rolnick

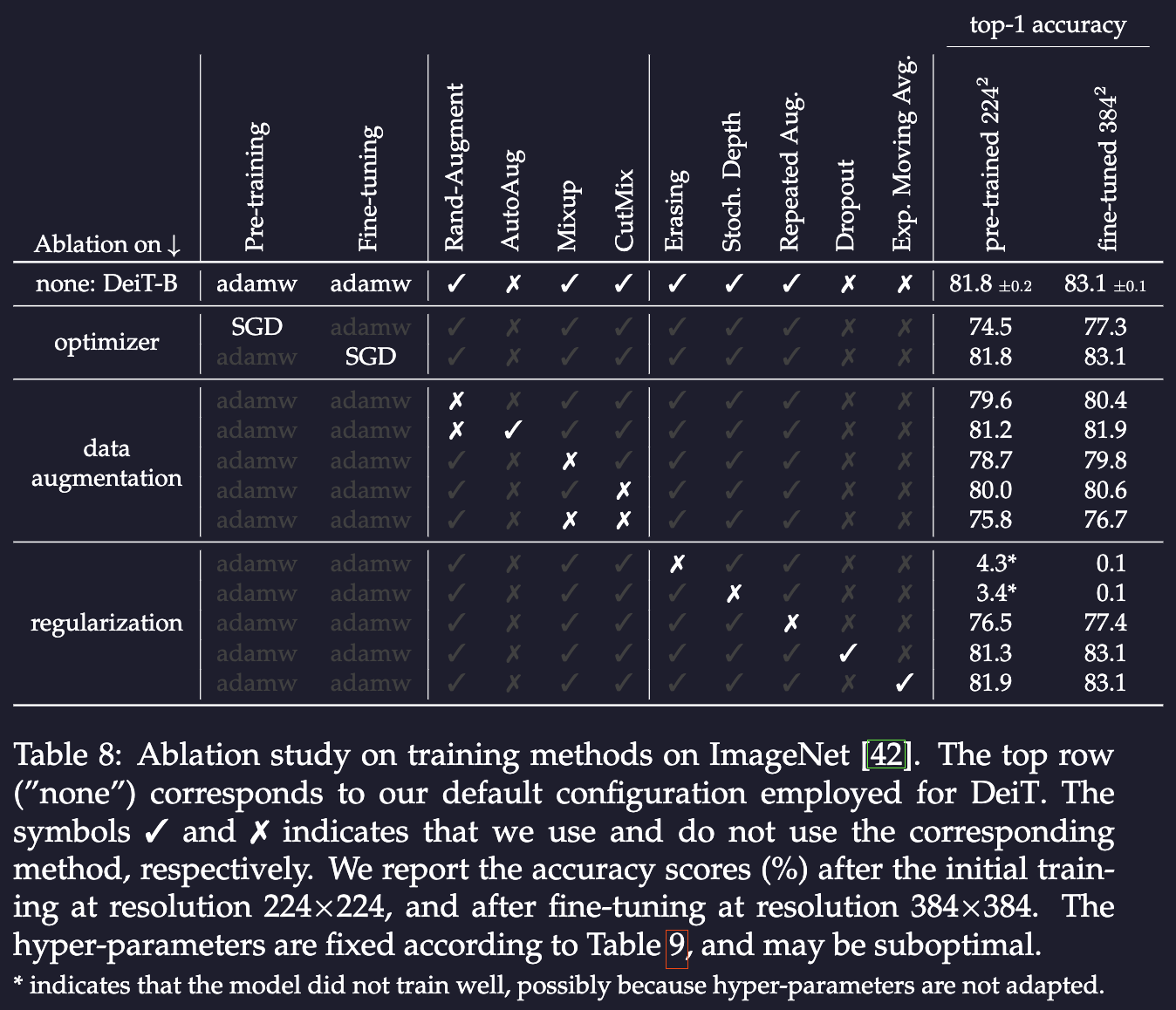
• almost all the data-augmentation methods that we evaluate prove to be useful. One exception is dropout, which we exclude from our training procedure. deit, page 15

• The used ones are Mixup, cutmix, Rand-Augment
• For regularization, Stochastic Depth, Repeated Augmentation, this one is mentioned in quite some places in the paper. In fact, timm’s RepeatedAugSampler is adapted from DeiT implementation.

Beating ViT on small model seems like an easy task. The big models are so big, they don’t even bother to do any augmentation, since there’s abundant of data.

DeiT⚗, the distilled model

The success has several key components: hard label distillation, token based distllation, fine tuning with higher resolution, joint classfier.

Some more on Knowledge Distilling

the teacher’s supervision takes into account the effects of the data augmentation, which sometimes causes a misalignment between the real label and the image. For example, let us consider image with a “cat” label that represents a large landscape and a small cat in a corner. If the cat is no longer on the crop of the data augmentation it implicitly changes the label of the image. KD can transfer inductive biases in a soft way in a student model using a teacher model where they would be incorporated in a hard way. For example, it may be useful to induce biases due to convolutions in a transformer model by using a convolutional model as teacher

deit, page 4

Hard label

Recall that in the Knowledge Distilling we are optimizing this thing (I admit that note is not detailed enough):

Soft distillation minimizes the Kullback-Leibler divergence between the softmax of the teacher and the softmax of the student model. Let $Z_t$ be the logits of the teacher model, $Z_s$ the logits of the student model. We denote by $\tau$ the temperature for the distillation, $\lambda$ the coefficient balancing the Kullback–Leibler divergence loss (KL) and the cross-entropy ($L_{CE}$) on ground truth labels $y$, and $\psi$ the softmax function. The distillation objective is

$${\mathcal{L}}_{\mathrm{global}}=(1-\lambda ){\mathcal{L}}_{\mathrm{CE}}(\psi (Z_{\mathrm{s}}),y)+\lambda {\tau }^2\mathrm{KL}(\psi (Z_{\mathrm{s}}/\tau ),\psi (Z_{\mathrm{t}}/\tau )).$$

Hard-label distillation. We introduce a variant of distillation where we take the hard decision of the teacher as a true label. Let $y_t={\text{argmax}}_c{Z}_t(c)$ be the hard decision of the teacher, the objective associated with this hard-label distillation is:

$${\mathcal{L}}_{\mathrm{global}}^{\text{hardDistill}}=\frac{1}{2}{\mathcal{L}}_{\mathrm{CE}}(\psi (Z_s),y)+\frac{1}{2}{\mathcal{L}}_{\mathrm{CE}}(\psi (Z_s),y_t).$$

The author does not have good reasoning of why this performs better than the traditional soft one. In the token section we’ll see how this is actually being trained.

Distillation token

Recall that in classic classifier ViT structure, we’ve got a class token as the first one in the input and we use the output as the “real output”. We can add another similar one, call it “distillation token”, which is very similar as the class one, except the training object is given by the distillation component of the loss. That means we are learn each of its component individually.

Recall the ${\mathcal{L}}_{global}^{hardDistll}$ above, the loss is really computed as:

        elif self.distillation_type == 'hard':
            distillation_loss = F.cross_entropy(outputs_kd, teacher_outputs.argmax(dim=1))
 
        loss = base_loss * (1 - self.alpha) + distillation_loss * self.alpha

That $Z_s$ in the formula are two different values from the network.

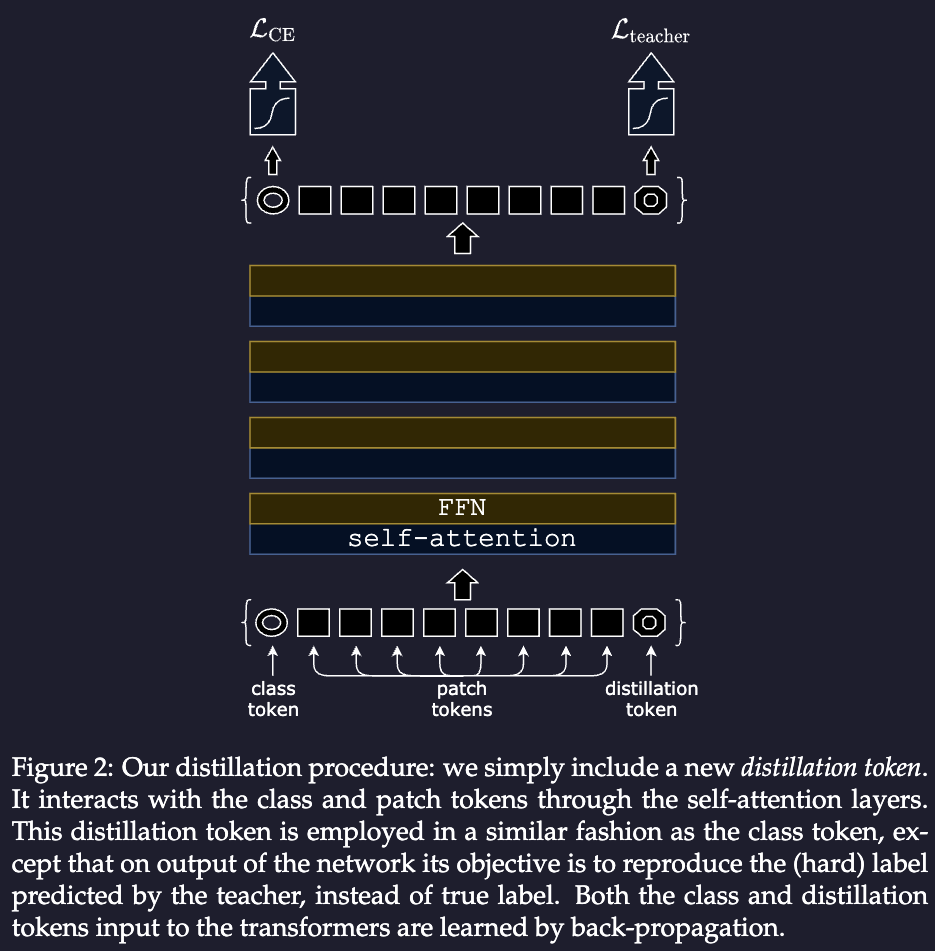. We then late fusion of these two separate heads by adding the predictions together. See the official implementation:

        if self.training:
            return x, x_dist
        else:
            # during inference, return the average of both classifier predictions
            return (x + x_dist) / 2

Fine tuning at higher resolution

TODO: Revisit this section after reading the FixEfficientNet paper. deit, page 8

We also interpolate the positional embeddings: In principle any classical image scaling technique, like bilinear interpolation, could be used. However, a bilinear interpolation of a vector from its neighbors reduces its $l_2-$norm compared to its neighbors. These low-norm vectors are not adapted to the pre-trained transformers and we observe a significant drop in accuracy if we employ use directly without any form of fine-tuning. Therefore we adopt a bicubic interpolation that approximately preserves the norm of the vectors, before fine-tuning the network with either AdamW or SGD.

deit, page 17

Discussion

We have observed that using a convnet teacher gives bet- ter performance than using a transformer. The fact that the convnet is a better teacher is probably due to the inductive bias inherited by the transformers through distillation

deit, page 9